
 我们刚刚学习的勾股定理是一个基本的平面几何定理,也是数学中最重要的定理之一.勾股定理其实有很多种方式证明.下图是1876年美国总统Garfield证明勾股定理所用的图形:
我们刚刚学习的勾股定理是一个基本的平面几何定理,也是数学中最重要的定理之一.勾股定理其实有很多种方式证明.下图是1876年美国总统Garfield证明勾股定理所用的图形:分析 用三角形的面积和、梯形的面积来表示这个图形的面积,从而证明勾股定理.
解答 解:∵Rt△ACB≌Rt△BDE,
∴∠CAB=∠DBE.
∵∠CAB+∠ABC=90°,
∴∠ABC+∠DBE=90°.
∴∠ABE=180°-90o=90o.
∴△ABE是一个等腰直角三角形,S△ABE=$\frac{1}{2}$c2.
又∵S梯形ACDE=$\frac{1}{2}$(a+b)2,
S梯形ACDE=S△ABC+S△BDE+S△ABE=ab+$\frac{1}{2}$c2.
∴$\frac{1}{2}$(a+b)2=ab+$\frac{1}{2}$c2,
即a2+b2=c2.
由此验证勾股定理.
点评 此题考查了勾股定理的证明,此题主要利用了三角形的面积公式:底×高÷2,和梯形的面积公式:(上底+下底)×高÷2证明勾股定理.


科目:初中数学 来源: 题型:解答题
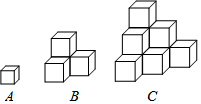
| 层数 | 1 | 2 | 3 | 4 | … | n |
| t | 1 | 3 | 6 | 10 | … | $\frac{n(n+1)}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
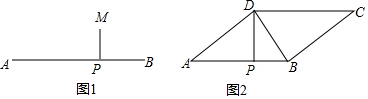
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{AD}{AB}$=$\frac{DE}{BC}$ | B. | $\frac{CE}{AE}$=$\frac{AD}{BD}$ | C. | $\frac{AB}{BD}$=$\frac{DE}{BC}$ | D. | $\frac{AE}{AD}$=$\frac{AC}{AB}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条直角边对应相等的两个直角三角形全等 | |
| B. | 一条边和一个锐角对应相等的两个三角形全等 | |
| C. | 有两边和其中一边的对角(此角为钝角)对应相等的两个三角形全等 | |
| D. | 有两条边对应相等的两个直角三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
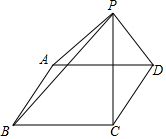 如图,平行四边形ABCD的两个高分别为3cm和4cm,P为平行四边形ABCD外一点,三角形PBC的面积为20cm2,三角形PAD的面积为8cm2,求平行四边形ABCD的周长?
如图,平行四边形ABCD的两个高分别为3cm和4cm,P为平行四边形ABCD外一点,三角形PBC的面积为20cm2,三角形PAD的面积为8cm2,求平行四边形ABCD的周长?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com