
| A. | 6$\sqrt{2}$ | B. | 10 | C. | 8 | D. | $\sqrt{31}$ |
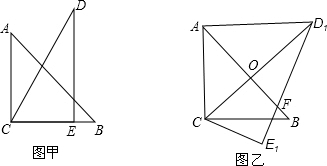
分析 先求出∠ACD=30°,再根据旋转角求出∠ACD1=45°,然后判断出△ACO是等腰直角三角形,再根据等腰直角三角形的性质求出AO、CO,AB⊥CO,再求出OD1然后利用勾股定理列式计算即可得解.
解答 解:∵∠ACB=∠DEC=90°,∠D=30°,
∴∠DCE=90°-30°=60°,
∴∠ACD=90°-60°=30°,
∵旋转角为15°,
∴∠ACD1=30°+15°=45°,
又∵∠A=45°,
∴△ACO是等腰直角三角形,
∴AO=CO=$\frac{1}{2}$AB=$\frac{1}{2}$×12=6,AB⊥CO,
∵DC=14,
∴D1C=DC=14,
∴D1O=14-6=8,
在Rt△AOD1中,AD1=$\sqrt{A{D}^{2}+{D}_{1}{O}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
故选:B.
点评 本题考查了旋转的性质,等腰直角三角形的判定与性质,勾股定理的应用,根据等腰直角三角形的性质判断出AB⊥CO是解题的关键,也是本题的难点.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:解答题
 如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.
如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
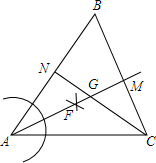 如图,在△ABC中,∠B=60°.以点A为圆心,任意长为半径画弧分别交AB、AC于点D、E,分别以点D、E为圆心,以大于$\frac{1}{2}$DE长为半径画弧,两弧相交于点F,作射线AF与BC相交于点M;
如图,在△ABC中,∠B=60°.以点A为圆心,任意长为半径画弧分别交AB、AC于点D、E,分别以点D、E为圆心,以大于$\frac{1}{2}$DE长为半径画弧,两弧相交于点F,作射线AF与BC相交于点M;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
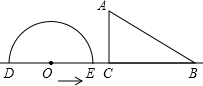 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的左侧,OC=8cm.(提示:直角三角形中,30度所对的直角边是斜边的一半,反之成立)
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的左侧,OC=8cm.(提示:直角三角形中,30度所对的直角边是斜边的一半,反之成立)查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷(解析版) 题型:单选题
把一元二次方程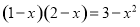 化成一般形式
化成一般形式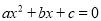 (a≠0),其中a、b、c 的值分别为( )
(a≠0),其中a、b、c 的值分别为( )
A. 2、3、﹣1 B. 2、﹣3、1 C. 2、﹣3、﹣1 D. 2、3、1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com