
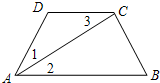
 如图已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由.
如图已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由.  开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6$\sqrt{2}$ | B. | 10 | C. | 8 | D. | $\sqrt{31}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
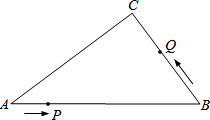 如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.
如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
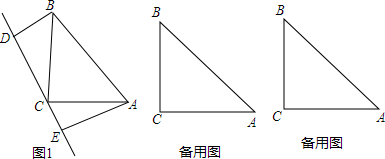
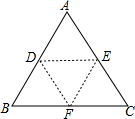 已知△ABC为等边三角形,D、E、F分别为AB边、AC边、BC边的中点,且小三角形EDF的面积为6cm2,将△ABC沿DE、EF、DF折叠后能拼成一个什么立体图形?拼成的立体图形的表面积是多少?
已知△ABC为等边三角形,D、E、F分别为AB边、AC边、BC边的中点,且小三角形EDF的面积为6cm2,将△ABC沿DE、EF、DF折叠后能拼成一个什么立体图形?拼成的立体图形的表面积是多少?查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:判断题
(本题满分8分)
如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[-2,1],求此函数图象的顶点坐标.
(2)探究下列问题:①若一个函数的特征数为[4,-1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com