
【题目】经销商购进某种商品,当购进量在20千克~50千克之间(含20千克和50千克)时,每千克进价是5元;当购进量超过50千克时,每千克进价是4元.此种商品的日销售量y(千克)受销售价x(元/千克)的影响较大,该经销商试销一周后获得如下数据:
x(元/千克) | 5 | 5.5 | 6 | 6.5 | 7 |
y(千克) | 90 | 75 | 60 | 45 | 30 |
解答下列问题:
(1)求出y关于x的一次函数表达式:
(2)若每天购进的商品能够全部销售完,且当日销售价不变,日销售利润为w元,那么销售价定为多少时,该经销商销售此种商品的当日利润最大?最大利润为多少元?此时购进量应为多少千克?(注:当日利润=(销售价-进货价)×日销售量).
【答案】(1)y=-30x+240(2)当销售价为6元时,经销商销售此种商品的当日利润最大,最大利润为120元,此时购进量应为60千克
【解析】
(1)根据待定系数法即可求解y关于x的一次函数表达式;
(2)先根据题意列出w关于x的二次函数,求出其最值,故可求解.
(1)设y关于x的一次函数表达式为y=kx+b(k≠0)
把(5,90),(6,60)代入得![]()
解得![]()
∴y关于x的一次函数表达式为y=-30x+240;
(2)当购进量在20千克~50千克之间(含20千克和50千克)时,
w1=(x-5)(-30x+240)=-30(x-6.5)2+67.5,
∵-30<0,∴x=6.5时,y=45kg, 日销售利润为67.5元;
当购进量超过50千克时,
w2=(x-4)(-30x+240)=-30(x-6)2+120,
∵-30<0,∴x=6时,y=60kg, 日销售利润为120元;
答:当销售价为6元时,经销商销售此种商品的当日利润最大,最大利润为120元,此时购进量应为60千克.


科目:初中数学 来源: 题型:
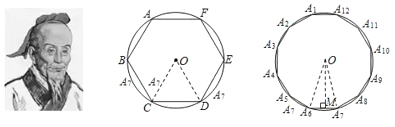
【题目】我国魏晋时期的数学家刘徽(263年左右)首创“割圆术”,所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率,刘徽计算出圆周率![]() .刘微从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割得越细,正多边形就越接近圆.设圆的半径为
.刘微从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割得越细,正多边形就越接近圆.设圆的半径为![]() ,圆内接正六边形的周长
,圆内接正六边形的周长![]() ,计算
,计算![]() ;圆内接正十二边形的周长
;圆内接正十二边形的周长![]() ,计算
,计算![]() ;那么分割到圆内接正二十四边形后,通过计算可以得到圆周率
;那么分割到圆内接正二十四边形后,通过计算可以得到圆周率![]() __________.(参考数据:
__________.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,四边形ABCD是正方形,∠MAN=90°,将∠MAN绕顶点A旋转,旋转角为∠DAM(0°<∠DAM<45°),AM交CD于点E,∠MAN的平分线与CB交于点G
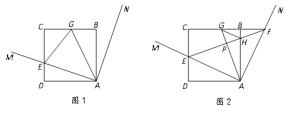
(1)证明:如图1,连接GE.求证:GE=DE+BG;
(2)探究:如图2,设AN交CB的延长线于点F,直线EF分别交AG,AB于点P,H.探究GH与AE的位置关系,并证明你的结论;
(3)应用:在图2中,若正方形的边长为6,BG=2,求GH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
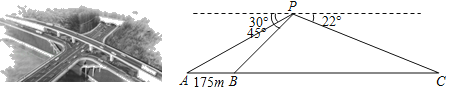
【题目】横卧于清波之上的黄石大桥与已经贯通的五峰山隧道将成为恩施城区跨越东西方向的最大直线通道,它把六角亭老城区与知名景点女儿城连为一体,缓解了恩施城区交通拥堵的现状.如图,某数学兴趣小组利用无人机在五峰山隧道正上空点P处测得黄石大桥西端点A的俯角为30°,东端点B(隧道西进口)的俯角为45°,隧道东出口C的俯角为22°,已知黄石大桥AB全长175米,隧道BC的长约多少米(计算结果精确到1米)?(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() 1.4,
1.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察以下等式:
第1个等式:![]() ; 第2个等式:
; 第2个等式:![]() ;
;
第3个等式:![]() ;第4个等式:
;第4个等式:![]() ;…
;…
按照以上规律,解决下列问题:
(1)写出第5个等式:_______________
(2)写出你猜想的第n个等式:________________________(用含n的等式表示),并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=![]() 的图象上,当-3≤x≤-1时,求函数值y的取值范围.
的图象上,当-3≤x≤-1时,求函数值y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标
,顶点坐标![]() 且开口向下,则下列结论:①抛物线经过点
且开口向下,则下列结论:①抛物线经过点![]() ;②
;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 有两个不相等的实数根;④对于任意实数
有两个不相等的实数根;④对于任意实数![]() ,
,![]() 总成立。其中结论正确的个数为( )
总成立。其中结论正确的个数为( )
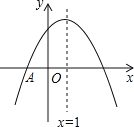
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
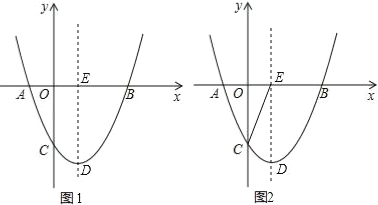
【题目】如图1,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣2),顶点为D,对称轴交x轴于点E.
(1)求该二次函数的解析式;
(2)设M为该抛物线对称轴左侧上的一点,过点M作直线MN∥x轴,交该抛物线于另一点N.是否存在点M,使四边形DMEN是菱形?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)连接CE(如图2),设点P是位于对称轴右侧该抛物线上一点,过点P作PQ⊥x轴,垂足为Q.连接PE,请求出当△PQE与△COE相似时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°.
(1)尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母)
①作线段AC的垂直平分线l,交AC于点O;
②连接BO并延长,在BO的延长线上截取OD,使得OD=OB;
③连接DA、DC.
(2)判断四边形ABCD的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com