
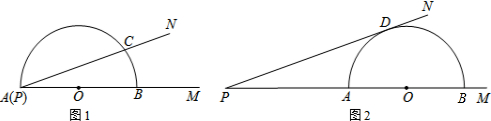
分析 (1)根据圆周角定理求出即可;
(2)根据切线的性质求出∠ACB=90°,解直角三角形求出PC即可;
(3)解直角三角形求出OP,即可求出PA,根据邻补角定义求出∠BOD即可.
解答 解:(1)∵已知点B,C,A处的读数分别为0,36.5°,180°,
∴∠BAC=$\frac{1}{2}$×36.5°=18.25°,
故答案为:18.25;
(2)连接BC,如图1,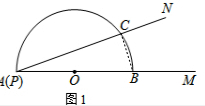
∵AB是直径,
∴∠ACB=90°,
∴$cos{18.25°}=\frac{PC}{AB}$,
PC=10×cos18.25°=10×0.95=9.5(cm);
﹙3﹚∵PN与圆切于D,连接OD,如图2,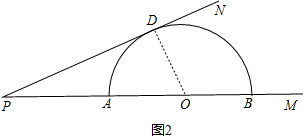
则OD⊥PN,
∵在Rt△PDO中,sin18.25°=$\frac{5}{OP}$,
∴OP=$\frac{5}{{sin{{18.25}°}}}=\frac{5}{0.313}≈15.97$,
∴PA=15.97-5=10.97,
∵∠BOD=90°+18.25°=108.25°,
∴切点D读数是108.25°,
所以平移大约10.97厘米后半圆量角器与PN相切于D,则切点D读数是108.25°.
点评 本题考查了圆周角定理,解直角三角形,切线的性质的应用,主要考查学生的理解能力和计算能力,注意:直径所对的圆周角是直角,圆的切线垂直于过切点的半径,有一定的难度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,弦CD与AB相交于E,DE=EC,过点B的切线与AF的延长线交于F,过E作EG⊥BC于G,延长CE交AD于H
如图,AB为⊙O的直径,弦CD与AB相交于E,DE=EC,过点B的切线与AF的延长线交于F,过E作EG⊥BC于G,延长CE交AD于H查看答案和解析>>
科目:初中数学 来源: 题型:解答题
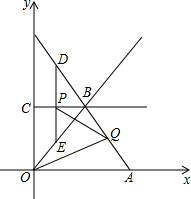 如图所示,A(8,0),B点在第一象限,且△AOB是等边三角形,过B点作直线BC∥x轴,交y轴于点C,动点P从C点出发,以每秒1个单位的速度向C点右侧水平方向平移,过P点作DE∥y轴,交直线AB于D,交直线OB于点E,设P点出发的时间为t秒.
如图所示,A(8,0),B点在第一象限,且△AOB是等边三角形,过B点作直线BC∥x轴,交y轴于点C,动点P从C点出发,以每秒1个单位的速度向C点右侧水平方向平移,过P点作DE∥y轴,交直线AB于D,交直线OB于点E,设P点出发的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
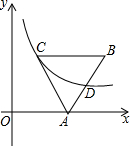 已知如图,边长为2的等边△ABC的顶点A在x轴的正半轴上,边BC∥x轴,点D为边AB的中点,双曲线y=$\frac{k}{x}$(k≠0)经过C、D两点,则k的值为( )
已知如图,边长为2的等边△ABC的顶点A在x轴的正半轴上,边BC∥x轴,点D为边AB的中点,双曲线y=$\frac{k}{x}$(k≠0)经过C、D两点,则k的值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
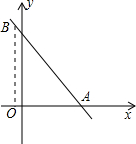 如图所示,平面直角坐标系中有一直线AB与x轴夹角为60°,且点A坐标为(3,0),点B在x轴上方,设AB=k,那么点B的横坐标为( )
如图所示,平面直角坐标系中有一直线AB与x轴夹角为60°,且点A坐标为(3,0),点B在x轴上方,设AB=k,那么点B的横坐标为( )| A. | 3-$\frac{k}{2}$ | B. | 3+$\frac{k}{2}$ | C. | $\frac{k}{2}$ | D. | -$\frac{k}{2}$-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com