
 如图,AB为⊙O的直径,弦CD与AB相交于E,DE=EC,过点B的切线与AF的延长线交于F,过E作EG⊥BC于G,延长CE交AD于H
如图,AB为⊙O的直径,弦CD与AB相交于E,DE=EC,过点B的切线与AF的延长线交于F,过E作EG⊥BC于G,延长CE交AD于H分析 (1)由AB为⊙O的直径,DE=EC,根据垂径定理的推论,可证得AB⊥CD,又由EG⊥BC,易证得∠CDA=∠DEH,即可得HD=EH,继而可证得AH=EH,则可证得结论;
(2)由AB为⊙O的直径,可得∠BDF=90°,由BF是切线,可得∠DBF=∠C,然后由三角函数的性质,求得BD的长,继而求得答案;
(3)根据题意得出DE,BE,EC的长,再利用三角形面积公式求出即可.
解答 (1)证明:∵AB为⊙O的直径,DE=EC,
∴AB⊥CD,
∴∠C+∠CBE=90°,
∵EG⊥BC,
∴∠C+∠CEG=90°,
∴∠CBE=∠CEG,
∵∠CBE=∠CDA,∠CEG=∠DEH,
∴∠CDA=∠DEH,
∴HD=EH,
∵∠A+∠ADC=90°,∠AEH+∠DEH=90°,
∴AH=EH,
∴AH=HD,
又∵∠AED=90°,
∴H为三角形ADE的外心;
(2)解:∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠BDF=90°,
∵BF是⊙O的切线,
∴∠DBF=∠C,
∵cos∠C=$\frac{4}{5}$,DF=9,
∴tan∠DBF=$\frac{3}{4}$,
∴BD=$\frac{DF}{tan∠DBF}$=12,
∵∠A=∠C,
∴sin∠A=$\frac{3}{5}$,
∴AB=$\frac{BD}{sinA}$=20,
∴⊙O的半径为10;
(3)解:∵BD=12,AB=20,∴AD=16,
则DE×AB=BD×AD,
即DE=$\frac{12×16}{20}$=$\frac{48}{5}$,
∵DE2=BE×AE,
∴($\frac{48}{5}$)2=BE(20-BE),
解得:BE1=12.8(不合题意舍去),BE2=7.2,
∵△AHE与△DBC的面积分别为S1,S2,
∴S1=$\frac{1}{2}$×$\frac{1}{2}$×AE×DE=$\frac{1}{4}$×12.8×$\frac{48}{5}$,
S2=$\frac{1}{2}$×DC×BE=$\frac{1}{2}$×$\frac{48}{5}$×2×7.2,
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{\frac{1}{4}×12.8×\frac{48}{5}}{\frac{1}{2}×\frac{48}{5}×2×7.2}$=$\frac{4}{9}$.
点评 此题考查了切线的性质、垂径定理、圆周角定理、弦切角定理、等腰三角形的判定与性质以及三角函数等知识.此题难度适中,注意掌握数形结合思想与转化思想的应用.


科目:初中数学 来源: 题型:解答题
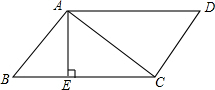 如图,在?ABCD中,AE⊥BC,垂足为E,且E为BC中点,若?ABCD的周长为20cm,△ABC的周长比?ABCD的周长少6cm,求?ABCD各边的长.
如图,在?ABCD中,AE⊥BC,垂足为E,且E为BC中点,若?ABCD的周长为20cm,△ABC的周长比?ABCD的周长少6cm,求?ABCD各边的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com