
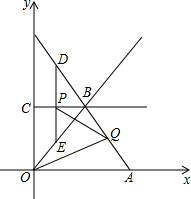
 如图所示,A(8,0),B点在第一象限,且△AOB是等边三角形,过B点作直线BC∥x轴,交y轴于点C,动点P从C点出发,以每秒1个单位的速度向C点右侧水平方向平移,过P点作DE∥y轴,交直线AB于D,交直线OB于点E,设P点出发的时间为t秒.
如图所示,A(8,0),B点在第一象限,且△AOB是等边三角形,过B点作直线BC∥x轴,交y轴于点C,动点P从C点出发,以每秒1个单位的速度向C点右侧水平方向平移,过P点作DE∥y轴,交直线AB于D,交直线OB于点E,设P点出发的时间为t秒.分析 (1)作FG⊥OA于点G,作QH⊥OA于点H,利用三角函数求的Q的坐标,则OQ即可求得,证明△OBQ∽△OQF,即可求得OF的长,进而利用三角函数求得F的坐标,利用待定系数法求得FQ的解析式,P的纵坐标是等边△OAB的高长,即可求得P的横坐标,从而求得t的值;
(2)求得AD和OB的解析式,即可利用t表示出DE的长,然后分当D或E是等腰直角三角形的直角顶点和M是等腰直角三角形的直角顶点两种情况进行讨论,求得t的值.
解答 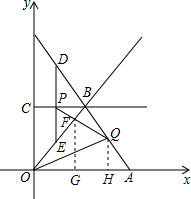 解:(1)作FG⊥OA于点G,作QH⊥OA于点H.
解:(1)作FG⊥OA于点G,作QH⊥OA于点H.
∵△OAB是等边三角形,
∴∠BOA=∠OBA=∠OAB=60°,
在直角△AQH中,QH=AQ•sin∠OAB=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$,AH=AQ•cos∠OAB=$\frac{1}{2}$×3=$\frac{3}{2}$,
∴OH=OA-AH=8-$\frac{3}{2}$=$\frac{13}{2}$,Q的坐标是($\frac{13}{2}$,$\frac{3\sqrt{3}}{2}$).
∴在直角△OQH中,OQ=$\sqrt{O{H}^{2}+Q{H}^{2}}$=$\sqrt{(\frac{13}{2})^{2}+(\frac{3\sqrt{3}}{2})^{2}}$=7.
∵∠OBA=∠OQP=60°,∠BOQ=∠QOF,
∴△OBQ∽△OQF,
∴$\frac{OF}{OQ}$=$\frac{OQ}{OB}$,即$\frac{OF}{7}$=$\frac{7}{8}$,
解得:OF=$\frac{49}{8}$.
在直角△OFG中,FG=OF•sin∠AOB=$\frac{49}{8}$×$\frac{\sqrt{3}}{2}$=$\frac{49\sqrt{3}}{16}$,
OG=OF•cos∠AOB=$\frac{49}{8}$×$\frac{1}{2}$=$\frac{49}{16}$.
则F的坐标是($\frac{49}{16}$,$\frac{49\sqrt{3}}{16}$).
设直线PQ的解析式是y=kx+b,
则$\left\{\begin{array}{l}{\frac{13}{2}k+b=\frac{3\sqrt{2}}{2}}\\{\frac{49}{16}k+b=\frac{49\sqrt{3}}{16}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{25\sqrt{3}}{3}}\\{b=\frac{167\sqrt{3}}{3}}\end{array}\right.$,
则直线PQ的解析式是y=-$\frac{25\sqrt{3}}{3}$x+$\frac{167\sqrt{3}}{3}$.
B的纵坐标是:8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$.
在y=-$\frac{25\sqrt{3}}{3}$x+$\frac{167\sqrt{3}}{3}$令y=4$\sqrt{3}$,
解得:.x=$\frac{31}{5}$.
则t=$\frac{31}{5}$;
(2)直线OB的解析式是y=$\sqrt{3}$x,
AB的解析式是:y=-$\sqrt{3}$x+8$\sqrt{3}$,
则当x=t时,PE=(-$\sqrt{3}$t+8$\sqrt{3}$)-$\sqrt{3}$t=8$\sqrt{3}$-2$\sqrt{3}$t.
当D或E是等腰直角三角形的直角顶点时,t=8$\sqrt{3}$-2$\sqrt{3}$t,解得:t=$\frac{48+8\sqrt{3}}{11}$.
当M是等腰直角三角形的直角顶点时,t=$\frac{1}{2}$(8$\sqrt{3}$-2$\sqrt{3}$t),
解得:t=6-2$\sqrt{3}$.
点评 本题是三角函数、等边三角形的性质、相似三角形的判定与性质以及待定系数法求函数的解析式的综合应用,正确求得F的坐标是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
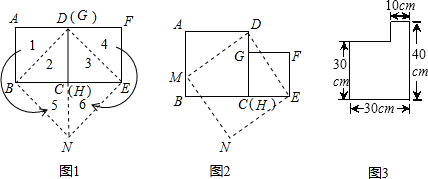
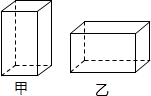 某纸品厂要制作如图所示的甲、乙两种无盖的长方体小盒,该长利用边角料裁出了长方形和正方形两种纸片,其中长方形纸片的宽与正方形纸片的边长相等,现用70张正方形纸片和180张长方形纸片制作这两种小盒(不计算连接部分),则可以制作甲、乙两种小盒各多少个?
某纸品厂要制作如图所示的甲、乙两种无盖的长方体小盒,该长利用边角料裁出了长方形和正方形两种纸片,其中长方形纸片的宽与正方形纸片的边长相等,现用70张正方形纸片和180张长方形纸片制作这两种小盒(不计算连接部分),则可以制作甲、乙两种小盒各多少个?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
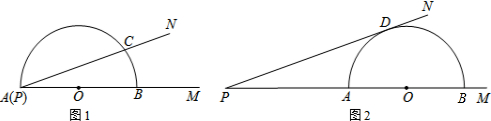
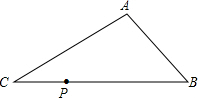 如图,已知点P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么D点的位置最多有( )
如图,已知点P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么D点的位置最多有( )| A. | 2处 | B. | 3处 | C. | 4处 | D. | 5处 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com