
【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点。

(1)求点A、B、C的坐标;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM.如图,点P在点Q左边,试用含m的式子表示矩形PQNM的周长;
(3)当矩形PQNM的周长最大时,m的值是多少?并求出此时的△AEM的面积。
【答案】(1)A(﹣3,0),B(1,0);(2)矩形PMNQ的周长=﹣2m2﹣8m+2;(3)m=﹣2,S=![]() .
.
【解析】
试题(1)利用函数图象与坐标轴的交点的求法,求出点A,B,C的坐标;
(2)先确定出抛物线对称轴,用m表示出PM,MN即可;
(3)由(2)得到的结论判断出矩形周长最大时,确定出m,进而求出直线AC解析式,即可;
试题解析:(1)由抛物线y=﹣x2﹣2x+3可知,C(0,3).
令y=0,则0=﹣x2﹣2x+3,
解得,x=﹣3或x=l,
∴A(﹣3,0),B(1,0).
(2)由抛物线y=﹣x2﹣2x+3可知,对称轴为x=﹣1.
∵M(m,0),
∴PM=﹣m2﹣2m+3,MN=(﹣m﹣1)×2=﹣2m﹣2,
∴矩形PMNQ的周长=2(PM+MN)=(﹣m2﹣2m+3﹣2m﹣2)×2=﹣2m2﹣8m+2.
(3)∵﹣2m2﹣8m+2=﹣2(m+2)2+10,
∴矩形的周长最大时,m=﹣2.
∵A(﹣3,0),C(0,3),设直线AC的解析式y=kx+b,
∴![]() ,解得k=l,b=3,
,解得k=l,b=3,
∴解析式y=x+3,令x=﹣2,则y=1,
∴E(﹣2,1),
∴EM=1,AM=1,
∴S=![]() AM×EM=
AM×EM=![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线c:y=x2+2x﹣3,将抛物线c平移得到抛物线c′,如果两条抛物线,关于直线x=1对称,那么下列说法正确的是( )
A. 将抛物线c沿x轴向右平移![]() 个单位得到抛物线c′ B. 将抛物线c沿x轴向右平移4个单位得到抛物线c′
个单位得到抛物线c′ B. 将抛物线c沿x轴向右平移4个单位得到抛物线c′
C. 将抛物线c沿x轴向右平移![]() 个单位得到抛物线c′ D. 将抛物线c沿x轴向右平移6个单位得到抛物线c′
个单位得到抛物线c′ D. 将抛物线c沿x轴向右平移6个单位得到抛物线c′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解某年级1200名学生每学期参加社会实践活动时间,随机对该年级50名学生进行了调查,结果如下表:
时间(天) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
人 数 | 1 | 2 | 4 | 5 | 7 | 11 | 8 | 6 | 4 | 2 |
(1)在这个统计中,众数是 ,中位数是 ;
(2)补全下面的频率分布表和频率分布直方图:
分组 | 频数 | 频率 |
3.5~5.5 | 3 | 0.06 |
5.5~7.5 | 9 | 0.18 |
7.5~9.5 | 0.36 | |
9.5~11.5 | 14 | |
11.5~13.5 | 6 | 0.12 |
合 计 | 50 | 1.00 |

(3)请你估算这所学校该年级的学生中,每学期参加社会实践活动时间不少于9天的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为线段
为线段![]() 上一点,
上一点,![]() ,
, ![]() ,过点
,过点![]() 作直线
作直线![]() ,
,![]() ,在线段
,在线段![]() 上有一点
上有一点![]() ,使得
,使得![]() ,连接
,连接![]() ,若动点
,若动点![]() 从点
从点![]() 开始以每秒
开始以每秒![]() 个单位的速度按
个单位的速度按![]() 的路径运动,当运动到
的路径运动,当运动到![]() 点时停止运动,设出发的时间为
点时停止运动,设出发的时间为![]() 秒.
秒.

(1)当点![]() 在线段
在线段![]() 上运动时,若
上运动时,若![]() ,则
,则![]() 的值为_________;
的值为_________;
(2)求当![]() 为何值时,
为何值时,![]() 为等腰三角形;
为等腰三角形;
(3)若点![]() 为
为![]() 内部射线
内部射线![]() 上一点,当
上一点,当![]() 为等腰直角三角形,求线段
为等腰直角三角形,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图钢架中,焊上等长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是( )
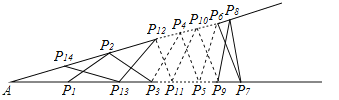
A.14B.13C.12D.11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有两条公路,一条是全长600km的普通公路,另一条是全长480km的高速公路,某客车在高速公路上行驶的平均速度比在普通公路上快45![]() /
/![]() ,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
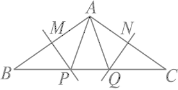
【题目】如图,在△ABC中,MP和NQ分别垂直平分AB和AC,
(1)若△APQ的周长为20,求BC的长;
(2)若∠BAC=110°,求∠PAQ的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学只有一张乒乓球比赛的门票,谁都想去,最后商定通过转盘游戏决定.游戏规则是:转动下面平均分成三个扇形且标有不同颜色的转盘,转盘连续转动两次,若指针前后所指颜色相同,则甲去;否则乙去.(如果指针恰好停在分割线上,那么重转一次,直到指针指向一种颜色为止)
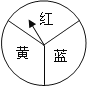
(1)转盘连续转动两次,指针所指颜色共有几种情况?通过画树状图或列表法加以说明;
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com