
����Ŀ���ס�����ͬѧֻ��һ��ƹ�����������Ʊ��˭����ȥ������̶�ͨ��ת����Ϸ��������Ϸ�����ǣ�ת������ƽ���ֳ����������ұ��в�ͬ��ɫ��ת����ת������ת����������ָ��ǰ����ָ��ɫ��ͬ�����ȥ��������ȥ�������ָ��ǡ��ͣ�ڷָ���������ô��תһ����ֱ��ָ��ָ��һ����ɫΪֹ��
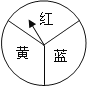
��1��ת������ת��������ָ����ָ��ɫ���м��������ͨ������״ͼ���б�������˵����
��2������Ϊ�����Ϸ��ƽ����˵��������
���𰸡���1��9����2�������Ϸ����ƽ��
��������
������������⿼����������еĹ�ƽ���������������Ĺؼ��Ǽ������������ĸ�����Ȼ��Ƚϼ�����
�����������1������״ͼ���£���

����ͼ��֪���ܹ���9�������
��2������ƽ��
���ɣ�����1����֪���ܹ���9�ֲ�ͬ����������dz��ֵĿ�������ͬ��������ɫ��ͬ����3����
����P����ȥ��=![]() ��P����ȥ��=
��P����ȥ��=![]() ��
��
��![]() ��
��![]() ��
��
�������Ϸ����ƽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2��2x+3��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ�����

��1�����A��B��C�����ꣻ
��2����M��m��0��Ϊ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N���ɵþ���PQNM����ͼ����P�ڵ�Q��ߣ����ú�m��ʽ�ӱ�ʾ����PQNM���ܳ���
��3��������PQNM���ܳ����ʱ��m��ֵ�Ƕ��٣��������ʱ����AEM�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD��������ABCD�ĶԽ��ߣ�BC=2����BC�������ڵ�ֱ����ƽ�ƣ���ͨ��ƽ�Ƶõ����߶μ�ΪPQ������PA��QD��������Q��QO��BD������ΪO������OA��OP��
��1����ֱ��д���߶�BC��ƽ�ƹ����У��ı���APQD��ʲô�ı��Σ�
��2�����ж�OA��OP֮���������ϵ��λ�ù�ϵ��������֤����
��3����ƽ�Ʊ任�����У���y=S��OPB��BP=x��0��x��2������y��x֮��ĺ�����ϵʽ�������y�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����мס��������յ���װ�ӷֱ�ΪA��B������˾��װ�յ����װ�װ��ΪA��˾��װ66̨�յ����Ұ�װ��ΪB��˾��װ80̨�յ����Ұ�װ����ǰһ�쿪���������װ�װ��ǡ��ͬʱ��ɰ�װ������֪�ӱ��Ҷ�ƽ��ÿ��లװ2̨�յ�����ס���������װ��ƽ��ÿ�����װ����̨�յ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��һ�ȵĹ���ѧ�����ʲ����У�������ѧ��ȫУ2000��������1000m���Գɼ������˳�飬ѧУ�ӳ����꼶��ȡ��һ���������ijɼ��������Ƴ�ͳ�Ʊ������Ƴ�Ƶ��ֱ��ͼ��
��� | ��Χ����λ���룩 | Ƶ�� | Ƶ�� |
1 | 170��x��200 | 5 | 0.1 |
2 | 200��x��230 | 13 | a |
3 | 230��x��260 | 15 | 0.3 |
4 | 260��x��290 | c | d |
5 | 290��x��320 | 5 | 0.1 |
6 | 320��x��350 | 2 | 0.04 |
7 | 350��x��380 | 2 | 0.04 |
�ϼ� | b | 1.00 |
��1������������У�������ʲô��
��2��ֱ��д��a��b��c��d��ֵ��
��3����ȫƵ��ֱ��ͼ��
��4�����б�ҵ�����ܲ�����Ŀ�ɼ�������������1000m������4��20�壨��260�룩Ϊ�ϸ����ܹ��Ƴ���У����������1000m�ĺϸ�����������ܣ�������ϸ��������������ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
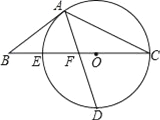
����Ŀ����ͼ���ԡ�ABC��BC����һ��OΪԲ�ģ�����A��C��������BC�߽��ڵ�E����DΪCE���°�Բ�����е㣬����AD���߶�EO�ڵ�F����AB=BF��
��1����֤��AB����O�����ߣ�
��2����CF=4��DF=![]() �����O�İ뾶r��sinB��
�����O�İ뾶r��sinB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a+b=1��ab=-1.��![]()
��1������S2��
��2�����Ķ��������S3�Ĺ��̣� ![]()
=![]()
=![]()
=![]()
��a+b=1��ab=-1��
��![]() _______.
_______.
��������������������ɣ�2����S3�ļ��������ټ���S4��
��3�����벢д��![]() ��
�� ![]() ��
�� ![]() ����֮���������ϵ����Ҫ��֤������n�Dz�С��2����Ȼ���������ݵó���������ϵ����S3.
����֮���������ϵ����Ҫ��֤������n�Dz�С��2����Ȼ���������ݵó���������ϵ����S3.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ�������ηָ��һ�������κ�����ȫ�ȵ�ֱ�������Σ���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ����������
����������![]() ��
�У�![]() .
.

̽��1
��1��С���������������α߳��ķ�����������ɵ�![]() ��
��![]() ����Ϊ
����Ϊ![]() ������
������![]() �����
�����![]()
̽��2
��2��С����������һ���������α߳��ķ���������![]() ������
������![]() ���Եõ�
���Եõ�![]() ��
��![]() �Ĺ�ϵ.�����С����˼·�������������.
�Ĺ�ϵ.�����С����˼·�������������.
̽��3
��3������С����С���õ��Ľ�����֤���ɶ���.��ע�����ݱ����Ļ������ʣ���![]() �ɵ�
�ɵ�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��x+1��x�ᣬy��ֱ���B��A���㣬����P���߶�AB���ƶ�����PΪ��������OPQ=45����x���ڵ�Q��

��1�����A�͵�B�����ꣻ
��2���Ƚ���AOP����BPQ�Ĵ�С��˵�����ɣ�
��3���Ƿ���ڵ�P��ʹ����OPQ�ǵ��������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com