
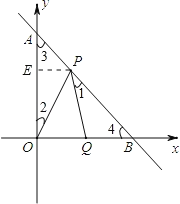
【题目】如图,直线y=﹣x+1与x轴,y轴分别交于B,A两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°交x轴于点Q.

(1)求点A和点B的坐标;
(2)比较∠AOP与∠BPQ的大小,说明理由.
(3)是否存在点P,使得△OPQ是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)A(0,1),B(1,0);(2)∠AOP=∠BPQ,理由详见解析;(3)点P坐标为(0,1),(![]() )或(1
)或(1![]() )时,△OPQ是等腰三角形.
)时,△OPQ是等腰三角形.
【解析】
(1)根据直线y=﹣x+1即可求得A、B的坐标;
(2)根据OA=OB,求得△AOB是等腰直角三角形,得出∠OAB=∠OBA=45°,根据三角形外角的性质即可得出结论.
(3)假设存在等腰三角形,分三种情况讨论:(ⅰ)OP=OQ;(ⅱ)QP=QO;(ⅲ)PO=PQ.能求出P点坐标,则存在点P,否则,不存在.
(1)∵直线y=﹣x+1与x轴,y轴分别交于A,B两点,令x=0,则y=0+1=1,∴A(0,1),令y=0,则0=﹣x+1,解得:x=1,∴B(1,0).
(2)∠AOP=∠BPQ.理由如下:
∵A(0,1),B(1,0),∴OA=OB=1,∴∠OAB=∠OBA=45°.
∵∠OAP+∠AOP=∠OPB=∠OPQ+∠BPQ,∴45°+∠AOP=45°+∠BPQ,∴∠AOP=∠BPQ.
(3)△OPQ可以是等腰三角形.理由如下:
如图,过P点PE⊥OA交OA于点E.分三种情况讨论:
(ⅰ)若OP=OQ,则∠OPQ=∠OQP,∴∠POQ=90°,∴点P与点A重合,∴点P坐标为(0,1);
(ⅱ)若QP=QO,则∠OPQ=∠QOP=45°,所以PQ⊥QO,可设P(x,x)代入y=﹣x+1得x![]() ,∴点P坐标为(
,∴点P坐标为(![]() );
);
(ⅲ)若PO=PQ.
∵∠OPQ+∠1=∠2+∠3,而∠OPQ=∠3=45°,∴∠1=∠2.
又∵∠3=∠4=45°,∴△AOP≌△BPQ(AAS),PB=OA=1,∴AP![]() 1.
1.
由勾股定理求得:PE=AE=1![]() ,∴EO
,∴EO![]() ,∴点P坐标为(1
,∴点P坐标为(1![]() ).
).
综上所述:点P坐标为(0,1),(![]() )或(1
)或(1![]() )时,△OPQ是等腰三角形.
)时,△OPQ是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,以原点O为圆心的圆交x轴于A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=20°,则∠OCD等于( )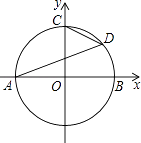
A.20°
B.40°
C.65°
D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为( )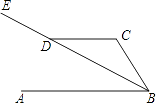
A.150°
B.130°
C.120°
D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(a,b)、B(c,d)、C(7,0),且![]()
(1)如果a1,d2,
①求A,B两点的坐标;
②求线段AB与y轴交点N的坐标,并求出△AOB的面积;
(2)如果b1,且△AOB与△ABC面积和为9,求a的值或取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用1200元购进一批服装,全部售完.由于服装畅销,服装店又用2800元,购进了第二批这种服装,所购数量是第一批购进量的2倍,但单价贵了5元,仍以同样的价格出售.卖了部分后,为了加快资金周转,服装店将剩余的20件以售价的八折全部出售.
问:(1)该服装店第一次购买了此种服装多少件?
(2)如果两批服装全部售完利润率不低于16%(不考虑其它因素),那么每件服装的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,正方形ABCD中的顶点B,D的坐标分别是(0,0),(2,0),且A,C两点关于x轴对称,则C点对应的坐标是( )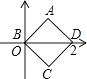
A.(1,1)
B.(1,﹣1)
C.(1,﹣2)
D.(2,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E,F,则线段B′F的长为( )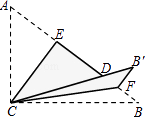
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①若![]() 则
则![]() ②若
②若![]() 则
则![]() ③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )
③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com