
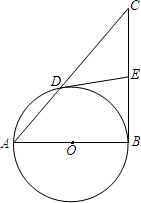 如图,已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连结DE.
如图,已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连结DE.分析 (1)只要证∠EDO=90°,即可得到DE是⊙O的切线;
(2)根据直角三角形两锐角互余得∠A=50°,根据cosA=$\frac{AD}{AB}$,即可求得⊙O的半径.
解答 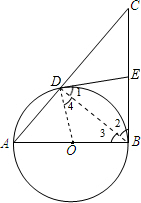 (1)证明:如图1,连接OD、DB;
(1)证明:如图1,连接OD、DB;
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=90°.
∵E为BC边上的中点,
∴CE=EB=DE,
∴∠1=∠2.
∵OB=OD,
∴∠3=∠4.
∴∠1+∠4=∠2+∠3.
∵在Rt△ABC中,∠ABC=∠2+∠3=90°,
∴∠EDO=∠1+∠4=90°.
∵D为⊙O上的点,
∴DE是⊙O的切线.
(2)解:∵∠ABC=90°,∠C=40°,
∴∠A=50°,
∵cosA=$\frac{AD}{AB}$,
∴AB=$\frac{AD}{cos50°}$=$\frac{6}{cos50°}$≈9.334,
∴⊙O的半径为4.67.
点评 主要考查了切线的判定方法和解直角三角函数.要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.


科目:初中数学 来源: 题型:选择题
| A. | y=-(x-1)2-3 | B. | y=-(x-1)2+3 | C. | y=-(x+1)2-3 | D. | y=-(x+1)2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -10 | +8 | -4 | +10 | +2 | +6 | -6 |
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 每天生产量(辆) | 190 | 208 | 196 | 210 | 202 | 206 | 194 |
 (2)该厂实行计件工资制,每生产一辆得60元,增产部分按每辆80元计算,减产部分按每辆50元计算,那么该厂工人这一周的工资总额是多少?
(2)该厂实行计件工资制,每生产一辆得60元,增产部分按每辆80元计算,减产部分按每辆50元计算,那么该厂工人这一周的工资总额是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com