
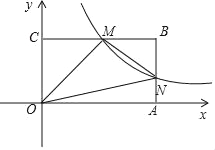
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x、y轴的正半轴上,顶点B的坐标为(4,2).点M是边BC上的一个动点(不与B、C重合),反比例函数y=![]() (k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
(k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
(1)当点M是边BC的中点时.
①求反比例函数的表达式;
②求△OMN的面积;
(2)在点M的运动过程中,试证明:![]() 是一个定值.
是一个定值.
【答案】(1)①y=![]() ;②3;(2)证明见解析.
;②3;(2)证明见解析.
【解析】
(1)①由矩形的性质及M是BC中点得出M(2,4),据此可得反比例函数解析式;
②先求出点N的坐标,从而得出CM=BM=2,AN=BN=1,再根据S△OMN=S矩形OABC﹣S△OAN﹣S△COM﹣S△BMN计算可得.
(2)设M(a,2),据此知反比例函数解析式为y=![]() ,求出N(4,
,求出N(4,![]() ),从而得BM=4﹣a,BN=2﹣
),从而得BM=4﹣a,BN=2﹣![]() ,再代入计算可得.
,再代入计算可得.
(1)①∵点B(4,2),且四边形OABC是矩形,
∴OC=AB=2,BC=OA=4,
∵点M是BC中点,
∴CM=2,
则点M(2,2),
∴反比例函数解析式为y=![]() ;
;
②当x=4时,y=![]() =1,
=1,
∴N(4,1),
则CM=BM=2,AN=BN=1,
∴S△OMN=S矩形OABC﹣S△OAN﹣S△COM﹣S△BMN
=4×2﹣![]() ×4×1﹣
×4×1﹣![]() ×2×2﹣
×2×2﹣![]() ×2×1
×2×1
=3;
(2)设M(a,2),
则k=2a,
∴反比例函数解析式为y=![]() ,
,
当x=4时,y=![]() ,
,
∴N(4,![]() ),
),
则BM=4﹣a,BN=2﹣![]() ,
,
∴![]() =
=![]() =
=![]() =2.
=2.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于A(﹣1,﹣1),B(2,﹣4)两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)请直接写出a,k,b的值及关于x的不等式ax2<kx﹣2的解集;
(2)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点C(0,2),它的顶点为D(1,m),且
与y轴交于点C(0,2),它的顶点为D(1,m),且![]() .
.
(1)求m的值及抛物线的表达式;
(2)将此抛物线向上平移后与x轴正半轴交于点A,与y轴交于点B,且OA=OB.若点A是由原抛物线上的点E平移所得,求点E的坐标;
(3)在(2)的条件下,点P是抛物线对称轴上的一点(位于x轴上方),且∠APB=45°.求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)“2015扬州鉴真国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”。小明和小刚参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组
(1)小明被分配到“迷你马拉松”项目组的概率为
(2)求小明和小刚被分配到不同项目组的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于一次函数y=5x﹣3的描述,下列说法正确的是( )
A. 图象经过第一、二、三象限B. 向下平移3个单位长度,可得到y=5x
C. 函数的图象与x轴的交点坐标是(0,﹣3)D. 图象经过点(1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
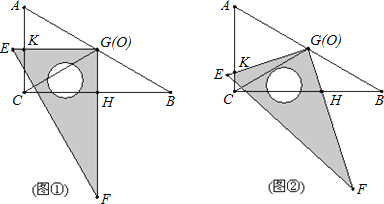
【题目】把两个全等的直角三角板ABC和EFG叠放在一起,使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,其中∠B=∠F=30°,斜边AB和EF长均为4.
(1)当 EG⊥AC于点K,GF⊥BC于点H时(如图①),求GH:GK的值.
(2) 现将三角板EFG由图①所示的位置绕O点沿逆时针方向旋转,旋转角α满足条件:0°<α<30°(如图②),EG交AC于点K ,GF交BC于点H,GH:GK的值是否改变?证明你发现的结论;
(3)三角板EFG由图①所示的位置绕O点逆时针旋转一周,是否存在某位置使△BFG是等腰三角形,若存在,请直接写出相应的旋转角α(精确到0.1°);若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
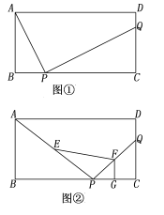
【题目】已知:如图①,②,在矩形ABCD中,AB=4,BC=8,P,Q分别是边BC,CD上的点.
(1)如图①,若AP⊥PQ,BP=2,求CQ的长;
(2)如图②,若![]() =2,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
=2,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是______度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com