
ЁОЬтФПЁПШчЭМЫљЪОЃЌвбжЊХзЮяЯпyЃНax2ЃЈaЁй0ЃЉгывЛДЮКЏЪ§yЃНkx+bЕФЭМЯѓЯрНЛгкAЃЈЉ1ЃЌЉ1ЃЉЃЌBЃЈ2ЃЌЉ4ЃЉСНЕуЃЌЕуPЪЧХзЮяЯпЩЯВЛгыAЃЌBжиКЯЕФвЛИіЖЏЕуЃЌЕуQЪЧyжсЩЯЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЧыжБНгаДГіaЃЌkЃЌbЕФжЕМАЙигкxЕФВЛЕШЪНax2ЃМkxЉ2ЕФНтМЏЃЛ
ЃЈ2ЃЉЕБЕуPдкжБЯпABЩЯЗНЪБЃЌЧыЧѓГіЁїPABУцЛ§ЕФзюДѓжЕВЂЧѓГіДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЪЧЗёДцдквдPЃЌQЃЌAЃЌBЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіPЃЌQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉaЃНЉ1ЃЌkЃНЉ1ЃЌbЃНЉ2ЃЌxЃМЉ1ЛђxЃО2ЃЛЃЈ2ЃЉЁїPABУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌДЫЪБЕуPЕФзјБъЮЊЃЈ
ЃЌДЫЪБЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉPЕФзјБъЮЊЃЈЉ3ЃЌЉ9ЃЉЛђЃЈ3ЃЌЉ9ЃЉЛђЃЈ1ЃЌЉ1ЃЉЃЌQЕФзјБъЮЊЃКQЃЈ0ЃЌЉ12ЃЉЛђЃЈ0ЃЌЉ6ЃЉЛђЃЈ0ЃЌЉ4ЃЉЃЎ
ЃЉЃЛЃЈ3ЃЉPЕФзјБъЮЊЃЈЉ3ЃЌЉ9ЃЉЛђЃЈ3ЃЌЉ9ЃЉЛђЃЈ1ЃЌЉ1ЃЉЃЌQЕФзјБъЮЊЃКQЃЈ0ЃЌЉ12ЃЉЛђЃЈ0ЃЌЉ6ЃЉЛђЃЈ0ЃЌЉ4ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУaЃЌkЃЌbЕФжЕЃЌИљОнЭМЯѓМДПЩЕУГіВЛЕШЪНЕФНтМЏЃЛЃЈ2ЃЉЙ§ЕуAзїyжсЕФЦНааЯпЃЌЙ§ЕуBзїxжсЕФЦНааЯпЃЌСНепНЛгкЕуCЃЌСЌНгPCЃЎЩшЕуPЕФКсзјБъЮЊmЃЌдђЕуPЕФзнзјБъЮЊЉm2ЃЎЙ§ЕуPзїPDЁЭACгкDЃЌзїPEЁЭBCгкEЃЎдђDЃЈЉ1ЃЌЉm2ЃЉЃЌEЃЈmЃЌЉ4ЃЉЃЌгЩДЫПЩЕУPDЃНm+1ЃЌPEЃНЉm2+4ЃЎдйИљОнSЁїAPBЃНSЁїAPC+SЁїBPCЉSЁїABCЃЌДњШыЪ§ОнМДПЩЕУSЁїAPBгыmЕФЖўДЮКЏЪ§ЙиЯЕЪНЃЌРћгУЖўДЮКЏЪ§ЧѓзюжЕЕФЗНЗЈЧѓЕУmЕФжЕМАSЁїAPB ЕФжЕзюДѓЃЎдйЧѓЕУЕуPЕФзјБъМДПЩЃЛЃЈ3ЃЉЃЈ3ЃЉИљОнЦНааЫФБпаЮЕФаджЪКЭзјБъЬиЕуНтД№МДПЩЃЎ
НтЃКЃЈ1ЃЉАбAЃЈЉ1ЃЌЉ1ЃЉЃЌДњШыyЃНax2жаЃЌПЩЕУЃКaЃНЉ1ЃЌ
АбAЃЈЉ1ЃЌЉ1ЃЉЃЌBЃЈ2ЃЌЉ4ЃЉДњШыyЃНkx+bжаЃЌПЩЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЫљвдaЃНЉ1ЃЌkЃНЉ1ЃЌbЃНЉ2ЃЌ
ЙигкxЕФВЛЕШЪНax2ЃМkxЉ2ЕФНтМЏЪЧxЃМЉ1ЛђxЃО2ЃЌ
ЃЈ2ЃЉЙ§ЕуAзїyжсЕФЦНааЯпЃЌЙ§ЕуBзїxжсЕФЦНааЯпЃЌСНепНЛгкЕуCЃЎ
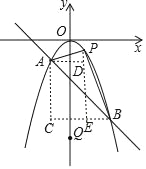
ЁпAЃЈЉ1ЃЌЉ1ЃЉЃЌBЃЈ2ЃЌЉ4ЃЉЃЌ
ЁрCЃЈЉ1ЃЌЉ4ЃЉЃЌACЃНBCЃН3ЃЌ
ЩшЕуPЕФКсзјБъЮЊmЃЌдђЕуPЕФзнзјБъЮЊЉm2ЃЎ
Й§ЕуPзїPDЁЭACгкDЃЌзїPEЁЭBCгкEЃЎдђDЃЈЉ1ЃЌЉm2ЃЉЃЌEЃЈmЃЌЉ4ЃЉЃЌ
ЁрPDЃНm+1ЃЌPEЃНЉm2+4ЃЎ
ЁрSЁїAPBЃНSЁїAPC+SЁїBPCЉSЁїABC
ЃН![]()
ЃН![]()
ЃН![]() ЃЎ
ЃЎ
Ёп![]() ЃМ0ЃЌ
ЃМ0ЃЌ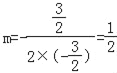 ЃЌЉ1ЃМmЃМ2ЃЌ
ЃЌЉ1ЃМmЃМ2ЃЌ
ЁрЕБ![]() ЪБЃЌSЁїAPB ЕФжЕзюДѓЃЎ
ЪБЃЌSЁїAPB ЕФжЕзюДѓЃЎ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌSЁїAPBЃН
ЃЌSЁїAPBЃН![]() ЃЌ
ЃЌ
МДЁїPABУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌДЫЪБЕуPЕФзјБъЮЊЃЈ
ЃЌДЫЪБЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
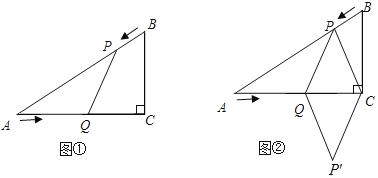
ЃЈ3ЃЉДцдкШ§зщЗћКЯЬѕМўЕФЕуЃЌ
ЕБвдPЃЌQЃЌAЃЌBЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌ
ЁпAPЃНBQЃЌAQЃНBPЃЌAЃЈЉ1ЃЌЉ1ЃЉЃЌBЃЈ2ЃЌЉ4ЃЉЃЌ
ПЩЕУзјБъШчЯТЃК
ЂйPЁфЕФКсзјБъЮЊЉ3ЃЌДњШыЖўДЮКЏЪ§БэДяЪНЃЌ
НтЕУЃКP'ЃЈЉ3ЃЌЉ9ЃЉЃЌQ'ЃЈ0ЃЌЉ12ЃЉЃЛ
ЂкPЁхЕФКсзјБъЮЊ3ЃЌДњШыЖўДЮКЏЪ§БэДяЪНЃЌ
НтЕУЃКPЁхЃЈ3ЃЌЉ9ЃЉЃЌQЁхЃЈ0ЃЌЉ6ЃЉЃЛ
ЂлPЕФКсзјБъЮЊ1ЃЌДњШыЖўДЮКЏЪ§БэДяЪНЃЌ
НтЕУЃКPЃЈ1ЃЌЉ1ЃЉЃЌQЃЈ0ЃЌЉ4ЃЉЃЎ
ЙЪЃКPЕФзјБъЮЊЃЈЉ3ЃЌЉ9ЃЉЛђЃЈ3ЃЌЉ9ЃЉЛђЃЈ1ЃЌЉ1ЃЉЃЌ
QЕФзјБъЮЊЃКQЃЈ0ЃЌЉ12ЃЉЛђЃЈ0ЃЌЉ6ЃЉЛђЃЈ0ЃЌЉ4ЃЉЃЎ


 ЦеЭЈИпжаЭЌВНСЗЯАВсЯЕСаД№АИ
ЦеЭЈИпжаЭЌВНСЗЯАВсЯЕСаД№АИ гХвэаЁАяЪжЭЌВНПкЫуЯЕСаД№АИ
гХвэаЁАяЪжЭЌВНПкЫуЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯABCЃН90ЁуЃЌЁЯACBЃН30ЁуЃЌACЃН6ЃЌЯжНЋRtЁїABCШЦЕуAЫГЪБеыа§зЊ30ЁуЕУЕНЁїABЁфCЁфЃЌдђЭМжавѕгАВПЗжУцЛ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЪОвтЭМЃЌаЁЛЊМвЃЈЕуAДІЃЉКЭЙЋТЗЃЈlЃЉжЎМфЪњСЂзХвЛПщ35mГЄЧвЦНаагкЙЋТЗЕФОоаЭЙуИцХЦЃЈDEЃЉЃЎЙуИцХЦЕВзЁСЫаЁЛЊЕФЪгЯпЃЌЧыдкЭМжаЛГіЪгЕуAЕФУЄЧјЃЌВЂНЋУЄЧјФкЕФФЧЖЮЙЋТЗМЦЮЊBCЃЎвЛСОвд60km/hдШЫйааЪЛЕФЦћГЕОЙ§ЙЋТЗЖЮЕФЪБМфЪЧ3sЃЌвбжЊЙуИцХЦКЭЙЋТЗЕФОрРыЪЧ40mЃЌЧѓаЁЛЊМвЕНЙЋТЗЕФОрРыЃЎЃЈОЋШЗЕН1mЃЉ
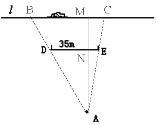
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌABЃН3cmЃЌвдBЮЊдВаФЃЌ1cmГЄЮЊАыОЖЛЁбBЃЌЕуPдкЁбBЩЯвЦЖЏЃЌСЌНгAPЃЌВЂНЋAPШЦЕуAФцЪБеыа§зЊ90ЁужСAPЁфЃЌСЌНгBPЁфЃЎдкЕуPвЦЖЏЕФЙ§ГЬжаЃЌBPЁфГЄЖШЕФзюаЁжЕЮЊ_____cmЃЎ
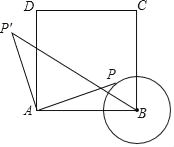
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
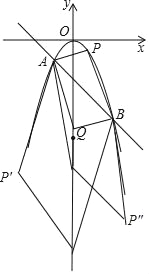
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=AC=5ЃЌBC=6ЃЌADЁЭBCЃЌДЙзуЮЊDЃЌЕуPЪЧБпABЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPFЁЮACНЛЯпЖЮBDгкЕуFЃЌзїPGЁЭABНЛADгкЕуEЃЌНЛЯпЖЮCDгкЕуGЃЌЩшBP=x.
ЃЈ1ЃЉгУКЌxЕФДњЪ§ЪНБэЪОЯпЖЮDGЕФГЄЃЛ
ЃЈ2ЃЉЩшЁїDEFЕФУцЛ§ЮЊ yЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЖЈвхгђЃЛ
ЃЈ3ЃЉЁїPEFФмЗёЮЊжБНЧШ§НЧаЮЃПШчЙћФмЃЌЧѓГіBPЕФГЄЃЛШчЙћВЛФмЃЌЧыЫЕУїРэгЩ.
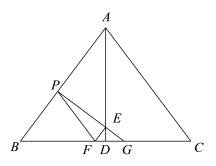
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіВЛЭИУїЕФПкДќРязАгаЗжБ№БъгаККзжЁАЪщЁБЁЂЁА ЯуЁБЁЂЁА РњЁБЁЂЁА ГЧЁБЕФЫФИіаЁЧђЃЌГ§ККзжВЛЭЌжЎЭтЃЌаЁЧђУЛгаШЮКЮЧјБ№ЃЌУПДЮУўЧђЧАЯШНСАшОљдШЃЎ
ЃЈ1ЃЉШєДгжаШЮШЁвЛИіЧђЃЌЧђЩЯЕФККзжИеКУЪЧ ЁАЪщЁБЕФИХТЪЮЊ__________.
ЃЈ2ЃЉДгжаШЮШЁвЛЧђЃЌВЛЗХЛиЃЌдйДгжаШЮШЁвЛЧђЃЌЧыгУЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓШЁГіЕФСНИіЧђЩЯЕФККзжФмзщГЩЁАРњГЧЁБЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЙ§ЕуAЃЈ6ЃЌ1ЃЉЃЎ
ЕФЭМЯѓЙ§ЕуAЃЈ6ЃЌ1ЃЉЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЙ§ЕуAЕФжБЯпгыЗДБШР§КЏЪ§yЃН![]() ЭМЯѓЕФСэвЛИіНЛЕуЮЊBЃЌгыyжсНЛгкЕуPЃЌШєAPЃН3PBЃЌЧѓЕуBЕФзјБъЃЎ
ЭМЯѓЕФСэвЛИіНЛЕуЮЊBЃЌгыyжсНЛгкЕуPЃЌШєAPЃН3PBЃЌЧѓЕуBЕФзјБъЃЎ
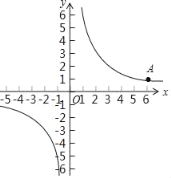
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпyЃНaЃЈxЉmЃЉ+kГЦЮЊХзЮяЯпyЃНaЃЈxЉmЃЉ2+kЕФЙиСЊжБЯпЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпyЃНx2+6xЉ1ЕФЙиСЊжБЯпЃЛ
ЃЈ2ЃЉвбжЊХзЮяЯпyЃНax2+bx+cгыЫќЕФЙиСЊжБЯпyЃН2x+3ЖМОЙ§yжсЩЯЭЌвЛЕуЃЌЧѓетЬѕХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ3ЃЉШчЭМЃЌЖЅЕудкЕквЛЯѓЯоЕФХзЮяЯпyЃНЉaЃЈxЉ1ЃЉ2+4aгыЫќЕФЙиСЊжБЯпНЛгкЕуAЃЌBЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыxжсИКАыжсНЛгкЕуCЃЌСЌНсACЁЂBCЃЎЕБЁїABCЮЊжБНЧШ§НЧаЮЪБЃЌЧѓaЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЂйЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃН8cmЃЌBCЃН6cmЃЌЕуPгЩBГіЗЂбиBAЗНЯђЯђЕуAдШЫйдЫЖЏЃЌЫйЖШЮЊ1cm/sЃЛЕуQгЩAГіЗЂбиACЗНЯђЯђЕуCдШЫйдЫЖЏЃЌЫйЖШЮЊ2cm/sЃЛСЌНгPQЃЎШєЩшдЫЖЏЕФЪБМфЮЊtЃЈsЃЉЃЈ0ЃМtЃМ4ЃЉЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌPQЁЮBCЃЛ
ЃЈ2ЃЉЩшЁїAQPЕФУцЛ§ЮЊyЃЈcm2ЃЉЃЌЧѓyгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЯпЖЮPQЧЁКУАбRtЁїACBЕФжмГЄКЭУцЛ§ЭЌЪБЦНЗжЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ4ЃЉШчЭМЂкЃЌСЌНгPCЃЌВЂАбЁїPQCбиQCЗелЃЌЕУЕНЫФБпаЮPQPЁфCЃЌФЧУДЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЫФБпаЮPQPЁфCЮЊСтаЮЃПШєДцдкЃЌЧѓГіДЫЪБСтаЮЕФБпГЄЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com