
����Ŀ��ij�̳�����һ��������ƽ��ÿ����۳�![]() ����ÿ��ӯ��
����ÿ��ӯ��![]() Ԫ��Ϊ���������ۣ�����ӯ�����̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣���һ����Χ�ڣ������ĵ���ÿ�½�
Ԫ��Ϊ���������ۣ�����ӯ�����̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣���һ����Χ�ڣ������ĵ���ÿ�½�![]() Ԫ���̳�ƽ��ÿ��ɶ��۳�
Ԫ���̳�ƽ��ÿ��ɶ��۳�![]() ����
����
![]() ����̳�ͨ��������������ÿ�����
����̳�ͨ��������������ÿ�����![]() Ԫ����ô�����ĵ���Ӧ�½�����Ԫ��
Ԫ����ô�����ĵ���Ӧ�½�����Ԫ��
![]() ��ÿ�������ĵ����½�����Ԫʱ��ÿ��ͨ�����۳�����õ���������������Ϊ����Ԫ��
��ÿ�������ĵ����½�����Ԫʱ��ÿ��ͨ�����۳�����õ���������������Ϊ����Ԫ��
���𰸡���1��ÿ������Ӧ��20Ԫ��
��2��ÿ����������15Ԫʱ���̳�ƽ��ÿ��Ӯ����࣬�������Ϊ1250Ԫ��
��������
��1������������=ÿ��������������з�������⼴����
��2����ÿ������ΪwԪ��ÿ������Ӧ����xԪ����������ɵ��������ʽ�����ú�������������ֵ��
��1��������ĵ���Ӧ�½�xԪ�����������
1200=��20+2x������40��x��
�����x=20��10����ÿ����۳���20+2x��=60��40����
��������x=20��10������������
��Ϊ����������������ӯ������xӦȡ20Ԫ��
���������ĵ���Ӧ�½�20Ԫ��
��2��w=��40��x����20+2x��=��2x2+60x+800=��2��x��15��2+1250
��x=15ʱ��ӯ�����Ϊ1250Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ֳ��ÿ�����ֳ�ɱ������̶��ɱ��Ϳɱ�ɱ������й̶��ɱ�ÿ���Ϊ4��Ԫ���ɱ�ɱ�������������֪����ֳ����һ��Ŀɱ�ɱ�Ϊ2.6��Ԫ����ɱ�ɱ�ƽ��ÿ�������İٷ���Ϊ![]()
��1���ú�x�Ĵ���ʽ��ʾ��3��Ŀɱ�ɱ�Ϊ ��Ԫ��
��2���������ֳ����3�����ֳ�ɱ�Ϊ7.146��Ԫ����ɱ�ɱ�ƽ��ÿ��������ٷ���x.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90����CD��AB�ڵ�D����E��ֱ��AC��һ���㣬����DE������D��FD��ED����ֱ��BC�ڵ�F.
(1)��ͼ1������E���߶�AC��ʱ����֤����DEC�ס�DFB.
(2)����E���߶�AC���ӳ�����ʱ��(1)�еĽ����Ƿ���Ȼ������������������ͼ2����֤����������������˵�����ɣ�
(3)��AC��![]() ��BC��2
��BC��2![]() ��DF��4
��DF��4![]() ����ֱ��д��CE�ij�.
����ֱ��д��CE�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
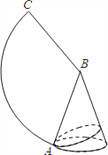
����Ŀ����ͼ,��֪Բ�ĵ���뾶��2,ĸ�߳���6.
��1�������Բ�ĸߺ������չ��ͼ����ABC�Ķ�����
��2�����A�ǵ���Բ����һ��,�ӵ�A��һ��������Բ����һȦ�ٻص�A��,��������ӵ���̳���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
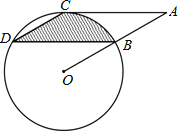
����Ŀ����ͼ����B��C��D����![]() �ϣ�����C��
�ϣ�����C��![]() ��OB�ӳ����ڵ�A������CD����
��OB�ӳ����ڵ�A������CD����![]() ��
��![]() ��
��
��1��ֱ��AC��![]() ��������λ�ù�ϵ��Ϊʲô��
��������λ�ù�ϵ��Ϊʲô��
��2��������CD��BD�뻡BC��Χ�ɵ���Ӱ���ֵ�������������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������Ա��10�����ѵ�����ɼ��ֱ��Ƴ���������ͳ��ͼ.
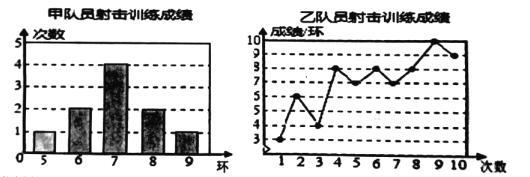
�����������������±���
ƽ���ɼ�/�� | ��λ��/�� | ����/�� | ���� | |
�� |
| 7 | 7 | 1.2 |
�� | 7 |
| 8 |
|
��1����![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��2���ֱ����ñ��е��ĸ�ͳ��������Ҫ������������Ա�����ѵ���ɼ�.��ѡ������һ������������ΪӦѡ������Ա��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ı߳�Ϊ2��
�ı߳�Ϊ2��![]() =60�����Խ���
=60�����Խ���![]() ��
��![]() �ཻ�ڵ�O���Ե�OΪ����ԭ�㣬�ֱ���
�ཻ�ڵ�O���Ե�OΪ����ԭ�㣬�ֱ���![]() ��
��![]() ����ֱ��Ϊx�ᡢy�ᣬ������ͼ��ʾ��ֱ������ϵ����
����ֱ��Ϊx�ᡢy�ᣬ������ͼ��ʾ��ֱ������ϵ����![]() Ϊ�Խ���������
Ϊ�Խ���������![]() ������
������![]() ������
������![]() Ϊ�Խ���������
Ϊ�Խ���������![]() ������
������![]() ������
������![]() Ϊ�Խ���������
Ϊ�Խ���������![]() ������
������![]() �������˹��ɼ�������ȥ����x����������ϵõ���
�������˹��ɼ�������ȥ����x����������ϵõ���![]() ��
��![]() ��
��![]() ����������������
����������������![]() �����
�����![]() ������Ϊ________��
������Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
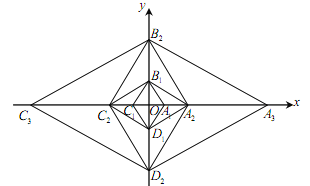
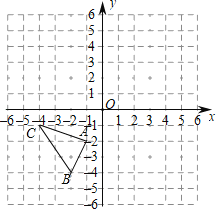
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���ABC���������������ֱ�ΪA����1����2����B����2����4����C����4����1����
��1����ƽ��ֱ������ϵ�л������ABC���ڵ�P��1��0�������ĶԳƵġ�A'B'C'�����ֱ�д����A'��B'��C'�����ꣻ
��2�������M��a��b���ǡ�ABC���ϣ�����A��B��C�غϣ�����һ�㣬��д���ڡ�A'B'C'�����M��Ӧ�ĵ�M'�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �У�
��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����תһ���ǶȺ�
˳ʱ����תһ���ǶȺ�![]() �Ķ�Ӧ��ǡ�����
�Ķ�Ӧ��ǡ�����![]() �غϣ��õ�
�غϣ��õ�![]() .
.
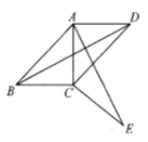
(1)�������ת�ǵĶ�����
(2)���ж�![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
(3)��![]() ��
��![]() ��������ı���
��������ı���![]() �ĶԽ���
�ĶԽ���![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com