
【题目】(本小题11分)完成下列推理说明:
(1)如图,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下:
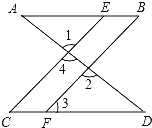
因为∠1=∠2(已知),且∠1=∠4(___________)
所以∠2=∠4(等量代换)
所以CE∥BF(___________)
所以∠___=∠3(_________________)
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD(______________________))
(2)如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.
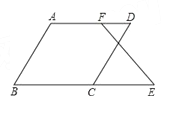
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD (__________)
∴∠B= ____(_______________________)
又∵∠B=∠D( 已知 ),
∴ ∠_____= ∠__________ ( 等量代换 )
∴AD∥BE(_____________________)
∴∠E=∠DFE(_____________________)
【答案】 对顶角相等 同位角相等,两直线平行 C 两直线平行,同位角相等 内错角相等,两直线平行 同旁内角互补,两直线平行 ∠DCE 两直线平行,同位角相等 ∠DCE ∠D 内错角相等,两直线平行 两直线平行,内错角相等
【解析】试题分析:(1)根据证平行的过程,一步步的将题中空缺部分补充完整即可;(2)根据平行线的判定和平行线的性质填空.
试题解析:
(1)如图,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下:
因为∠1=∠2(已知),且∠1=∠4( 对顶角相等 )
所以∠2=∠4(等量代换)
所以CE∥BF( 同位角相等,两直线平行 )
所以∠ C =∠3( 两直线平行,同位角相等 )
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD( 内错角相等,两直线平行 )
(2)在括号内填写理由.
如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD ( 同旁内角互补,两直线平行 )
∴∠B=∠DCE( 两直线平行,同位角相等 )
又∵∠B=∠D( 已知 ),
∴∠DCE=∠D ( 等量代换 )
∴AD∥BE( 内错角相等,两直线平行 )
∴∠E=∠DFE( 两直线平行,内错角相等 )


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是( )

A.②④ B.①④ C.②③ D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A(-1,0)、B(3,0)两点,直线y=x-2与x轴交于点D,与y轴交于点C.点P是x轴下方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
与x轴交于点A(-1,0)、B(3,0)两点,直线y=x-2与x轴交于点D,与y轴交于点C.点P是x轴下方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
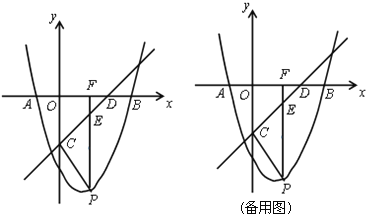
(1)求抛物线的解析式:
(2)若PE=3EF,求m的值;
(3)连接PC,是否存在点P,使△PCE为等腰直角三角形?若存在,请直接写出相应的点P的横坐标m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知将直线y=x+1向下平移3个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是( )
A.经过第一、二、四象限B.与x轴交于(2,0)
C.与直线y=2x+1平行D.y随的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个两位数的个位数字与十位数字对调,所得的两位数比原两位数小,且知个位数字与十位数字之和为6,则原来的两位数可能为_____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com