
【题目】已知:如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
【答案】(1)证明见解析;(2)矩形;证明见解析.
【解析】
试题分析:本题主要考查了平行四边形的基本性质和矩形的判定及全等三角形的判定.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.三角形全等的判定条件:SSS,SAS,AAS,ASA.
(1)在证明全等时常根据已知条件,分析还缺什么条件,然后用(SAS,ASA,SSS)来证明全等; (2)先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD是矩形.
试题解析:(1)∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=![]() AB,CF=
AB,CF=![]() CD.
CD.
∴AE=CF.
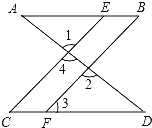
在△AED和△CBF中,
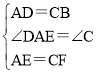 ,
,
∴△ADE≌△CBF(SAS).
(2)当四边形BEDF是菱形时,四边形AGBD是矩形.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形.


科目:初中数学 来源: 题型:
【题目】(本小题11分)完成下列推理说明:
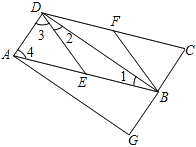
(1)如图,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下:
因为∠1=∠2(已知),且∠1=∠4(___________)
所以∠2=∠4(等量代换)
所以CE∥BF(___________)
所以∠___=∠3(_________________)
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD(______________________))
(2)如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.
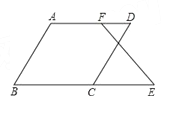
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD (__________)
∴∠B= ____(_______________________)
又∵∠B=∠D( 已知 ),
∴ ∠_____= ∠__________ ( 等量代换 )
∴AD∥BE(_____________________)
∴∠E=∠DFE(_____________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0)、
C(0,2),点B在第一象限。

(1)写出点B的坐标;
(2)若过点C的直线交长方形的OA边于点D,且把长方形OABC的周长分成2∶3的两部分,求点D的坐标;
(3)如果将(2)中的线段CD向下平移3个单位长度,得到对应线段C′D′,在平面直角坐标系中画出△CD′C′,并求出它的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织初二年级400名学生到威海参加拓展训练活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金250元,大客车每辆租金350元,请选出最省线的租车方案,并求出最少租金.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com