
【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍,我们把这条对角线叫做这个四边形的黄金线,这个四边形叫做黄金四边形.
(1)如图1,在四边形ABCD中,AB=AD=DC,对角线AC,BD都是黄金线,且AB<AC,CD<BD,求四边形ABCD各个内角的度数; 
(2)如图2,点B是弧AC的中点,请在⊙O上找出所有的点D,使四边形ABCD的对角线AC是黄金线(要求:保留作图痕迹); 
(3)在黄金四边形ABCD中,AB=BC=CD,∠BAC=30°,求∠BAD的度数.
【答案】
(1)解:∵在四边形ABCD中,对角线AC是黄金线,
∴△ABC是等腰三角形,
∵AB<AC,
∴AB=BC或AC=BC,
①当AB=BC时,
∵AB=AD=DC,
∴AB=BC=AD=DC,
又∵AC=AC,
∴△ABC≌△ADC,
此种情况不符合黄金四边形定义,
②AC=BC,
同理,BD=BC,
∴AC=BD=BC,易证得△ABD≌△DAC,△CAB≌△BDC,
∴∠DAC=∠DCA=∠ABD=∠ADB,∠BDC=∠BCD=∠CAB=∠CBA,
且∠DCA<∠DCB,
∴∠DAC<∠CAB
又由黄金四边形定义知:∠CAB=2∠DAC,
设∠DAC=∠DCA=∠ABD=∠ADB=x°,
则∠BDC=∠BCD=∠CAB=∠CBA=2x°,
∴∠DAB=∠ADC=3x°,
而四边形的内角和为360°,
∴∠DAB=∠ADC=108°,∠BCD=∠CBA=72°,
答:四边形ABCD各个内角的度数分别为108°,72°,108°,72°.
(2)解:由题意作图为:
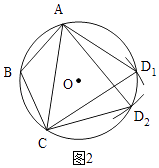
(3)解:∵AB=BC,∠BAC=30°,
∴∠BCA=∠BAC=30°,∠ABC=120°,
ⅰ)当AC为黄金线时,
∴△ACD是等腰三角形,
∵AB=BC=CD,AC>BC,
∴AD=CD或AD=AC,
当AD=CD时,则AB=BC=CD=AD,
又∵AC=AC,
∴△ABC≌△ADC,如图3,此种情况不符合黄金四边形定义,
∴AD≠CD,
当AD=AC时,由黄金四边形定义知,∠ACD=∠D=15°或60°,
此时∠BAD=180°(不合题意,舍去)或90°(不合题意,舍去);
ⅱ)当BD为黄金线时,
∴△ABD是等腰三角形,
∵AB=BC=CD,
∴∠CBD=∠CDB,
①当AB=AD时,△BCD≌△BAD,
此种情况不符合黄金四边形定义;
②当AB=BD时,AB=BD=BC=CD,
∴△BCD是等边三角形,
∴∠CBD=60°,
∴∠A=30°或120°(不合题意,舍去),
∴∠ABC=180°(不合题意,舍去),
此种情况也不符合黄金四边形定义;
③当AD=BD时,设∠CBD=∠CDB=y°,则∠ABD=∠BAD=(2y)°或 ![]() ,
,
∵∠ABC=∠CBD+∠ABD=120°,
当∠ABD=2y°时,y=40,
∴∠BAD=2y=80°;
当 ![]() 时,y=80,
时,y=80,
∴ ![]() ;
;
综上所述:∠BAD的度数为40°,80°.

【解析】(1))先由对角线AC是黄金线,可知△ABC是等腰三角形,分两种情况:①AB=BC,②AC=BC,第一种情况不成立,②设∠DAC=∠DCA=∠ABD=∠ADB=x°,则∠BDC=∠BCD=∠CAB=∠CBA=2x°,∠DAB=∠ADC=3x°,根据四边形内角和列等式可得x的值,计算各角的度数;(2)①以A为圆心,AC为半径画弧,交圆O于D1 , ②以C为圆心,AC为半径画弧,交圆O于D2 , ③连接AD1、CD1、AD2、CD2;(3)先根据∠BAC=30°,计算∠ABC=120°,分情况进行讨论:ⅰ)当AC为黄金线时,则AD=CD或AD=AC,根据等腰三角形的性质及黄金四边形定义进行计算即可;ⅱ)当BD为黄金线时,分三种情况: ①当AB=AD时;②当AB=BD时,③当AD=BD时,分别讨论即可.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市重庆路水果市场某水果店购进甲、乙两种水果.已知1千克甲种水果的进价比1千克乙种水果的进价多4元,购进2千克甲种水果与1千克乙种水果共需20元.
(1)求甲种水果的进价为每千克多少元?
(2)经市场调查发现,甲种水果每天销售量y(千克)与售价m(元/千克)之间满足如图所示的函数关系,求y与m之间的函数关系;
(3)在(2)的条件下,当甲种水果的售价定为多少元时,才能使每天销售甲种水果的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF. 
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(﹣1,0),顶点为(1,2),则结论:
①abc>0;②x=1时,函数最大值是2;③4a+2b+c>0;④2a+b=0;⑤2c<3b.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波轨道交通4号线已开工建设,计划2020年通车试运营.为了了解镇民对4号线地铁票的定价意向,某镇某校数学兴趣小组开展了“你认为宁波4号地铁起步价定为多少合适”的问卷调查,并将调查结果整理后制成了如下统计图,根据图中所给出的信息解答下列问题: 
(1)求本次调查中该兴趣小组随机调查的人数;
(2)请你把条形统计图补充完整;
(3)如果在该镇随机咨询一位居民,那么该居民支持“起步价为2元或3元”的概率是
(4)假设该镇有3万人,请估计该镇支持“起步价为3元”的居民大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,点B所经过的路径的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元.已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.由于出口需要,所有采购的大蒜必需在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半,为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F. 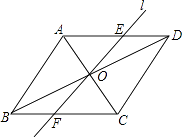
(1)求证:△AOE≌△COF;
(2)当α=30°时,求线段EF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com