
【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元.已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.由于出口需要,所有采购的大蒜必需在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半,为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?
【答案】
(1)解:设去年每吨大蒜的平均价格是x元,
由题意得, ![]() ×2=
×2= ![]() ,
,
解得:x=3500,
经检验:x=3500是原分式方程的解,且符合题意,
答:去年每吨大蒜的平均价格是3500元
(2)解:由(1)得,今年的大蒜数为: ![]() ×3=300(吨),
×3=300(吨),
设应将m吨大蒜加工成蒜粉,则应将(300﹣m)吨加工成蒜片,
由题意得, 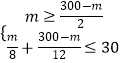 ,
,
解得:100≤m≤120,
总利润为:1000m+600(300﹣m)=400m+180000,
当m=120时,利润最大,为228000元.
答:应将120吨大蒜加工成蒜粉,最大利润为228000元
【解析】(1)设去年每吨大蒜的平均价格是x元,则第一次采购的平均价格为(x+500)元,第二次采购的平均价格为(x﹣500)元,根据第二次的采购数量是第一次采购数量的两倍,据此列方程求解;(2)先求出今年所采购的大蒜数,根据采购的大蒜必需在30天内加工完毕,蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半,据此列不等式组求解,然后求出最大利润.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现:小琼步行![]() 步与小刚步行
步与小刚步行![]() 步消耗的能量相同,若每消耗
步消耗的能量相同,若每消耗![]() 千卡能量小琼行走的步数比小刚多
千卡能量小琼行走的步数比小刚多![]() 步,求小刚每消耗
步,求小刚每消耗![]() 千卡能量需要行走多少步?
千卡能量需要行走多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2+4x﹣1=0,下列配方结果正确的是( )
A.(x+2)2=5
B.(x+2)2=1
C.(x﹣2)2=1
D.(x﹣2)2=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级二班在订购本班的班服前,按身高型号进行登记,对女生的记录中,身高150cm以下记为S号,150160cm以下记为M号,160170cm以下记为L号.170cm 以上记为XL号.若用统计图描述这些数据,合适的统计图是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2,2,3,4四个数中随机取两个数,第一个作为个位上的数字,第二个作为十位上的数字,组成一个两位数,则这个两位数是2的倍数的概率是 ( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com