练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某校七年级二班在订购本班的班服前，按身高型号进行登记，对女生的记录中，身高150cm以下记为S号，150160cm以下记为M号，160170cm以下记为L号．170cm 以上记为XL号．若用统计图描述这些数据，合适的统计图是 ．

    【答案】条形统计图
    【解析】解：为了清晰显示四种型号衣服的具体数量，应选用条形统计图，
    故答案为：条形统计图．
    条形统计图能很容易看出数量的多少；折线统计图不仅容易看出数量的多少，而且能反映数量的增减变化情况；扇形统计图能反映部分与整体的关系；由此根据情况选择即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】学校组织同学们春游，租用45座和30座两种型号的客车，若租用45座客车x辆，租用30座客车y辆，则不等式“45x＋30y≥500”表示的实际意义是(　　)

    A. 两种客车总的载客量不少于500人 B. 两种客车总的载客量不超过500人

    C. 两种客车总的载客量不足500人 D. 两种客车总的载客量恰好等于500人

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年我市某公司分两次采购了一批大蒜，第一次花费40万元，第二次花费60万元．已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元，第二次采购时每吨大蒜的价格比去年的平均价格下降了500元，第二次的采购数量是第一次采购数量的两倍．
    （1）试问去年每吨大蒜的平均价格是多少元？
    （2）该公司可将大蒜加工成蒜粉或蒜片，若单独加工成蒜粉，每天可加工8吨大蒜，每吨大蒜获利1000元；若单独加工成蒜片，每天可加工12吨大蒜，每吨大蒜获利600元．由于出口需要，所有采购的大蒜必需在30天内加工完毕，且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半，为获得最大利润，应将多少吨大蒜加工成蒜粉？最大利润为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a，b是方程x2﹣x﹣3=0的两个根，则代数式a2﹣（a+b）+b2的值为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x、y的二元一次方程组给出下列结论：①当k=5时，此方程组无解；②若此方程组的解也是方程6x+15y=16的解，则k=10；③无论整数k取何值，此方程组一定无整数解（x、y均为整数），其中正确的是（　　）
    A.①②③
    B.①③
    C.②③
    D.①②

    查看答案和解析>>

    科目：初中数学 来源： 题型：

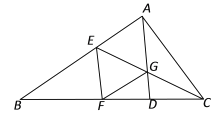
    【题目】如图，点D、E分别是△ABC边BC、AB上的点，AD、CE相交于点G，过点E作EF∥AD交BC于点F，且，联结FG.

    （1）求证：GF∥AB；

    （2）如果∠CAG=∠CFG，求证：四边形AEFG是菱形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(2017·齐齐哈尔中考)矩形ABCD的对角线AC，BD相交于点O，请你添加一个适当的条件________________，使其成为正方形(只填一个即可)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=ax2+bx﹣3交x轴于B、C两点，且B的坐标为（﹣2，0）直线y=mx+n过点B和抛物线上另一点A（4，3）
    （1）求抛物线和直线的解析式；
    （2）若点P为抛物线上的一个动点，且在直线AB下方，过P作PQ∥x轴，且PQ=4（点Q在P点右侧）．以PQ为一边作矩形PQEF，且点E在直线AB上．求矩形PQEF的最大值．并求出此时点P的坐标；
    （3）如图2，在（2）的结论下，连接AP、BP，设QE交于x轴于点D，现即将矩形PQEF沿射线DB以每秒1个单位长度的速度平移，当点D到达点B时停止，记平移时间为t，平移后的矩形PQEF为P′Q′E′F′，且Q′E′分别交直线AB、x轴于N、D′，设矩形P′Q′E′F′与△ABP的重叠部分面积为s，当NA= ND′时，求s的值．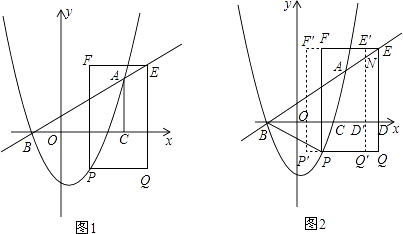

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校准备组织520名学生进行野外考察活动，行李共有240件．学校计划租用甲、乙两种型号的汽车共12辆，经了解，甲种汽车每辆最多能载50人和15件行李，乙种汽车每辆最多能载40人和25件行李．设租用甲种汽车辆，你认为下列符合题意的不等式组是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案