
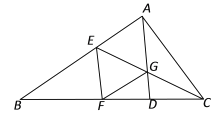
【题目】如图,点D、E分别是△ABC边BC、AB上的点,AD、CE相交于点G,过点E作EF∥AD交BC于点F,且![]() ,联结FG.
,联结FG.
(1)求证:GF∥AB;
(2)如果∠CAG=∠CFG,求证:四边形AEFG是菱形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由![]() ,可得
,可得![]() ,再由EF∥AD,根据平行线分线段成比例定理可得
,再由EF∥AD,根据平行线分线段成比例定理可得 ![]() ,所以
,所以![]() ,即可得GF∥AB ;(2)联结AF ,证明ΔCAD∽ΔCBA,根据相似三角形的性质可得
,即可得GF∥AB ;(2)联结AF ,证明ΔCAD∽ΔCBA,根据相似三角形的性质可得 ![]() ,即
,即![]() ,再因
,再因![]() ,即可得
,即可得![]() ,可得∠CAF=∠CFA,因∠CAG=∠CFG,可得∠GAF=∠GFA,即可得GA=GF,再由四边形AEFG是平行四边形,即可判断四边形AEFG是菱形.
,可得∠CAF=∠CFA,因∠CAG=∠CFG,可得∠GAF=∠GFA,即可得GA=GF,再由四边形AEFG是平行四边形,即可判断四边形AEFG是菱形.
试题解析:
(1)证明:∵![]() ,∴
,∴![]()
∵EF∥AD,∴ ![]()
∴![]()
∴GF∥AB
(2) 联结AF ,∵GF∥AB ∴![]()
∵![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ∽
∽![]()
∴ ![]() ,即
,即![]()
∵![]() ,∴
,∴![]()
∴![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()
∵GF∥AB,EF∥AD,∴四边形![]() 是平行四边形
是平行四边形
∴四边形![]() 是菱形
是菱形


科目:初中数学 来源: 题型:
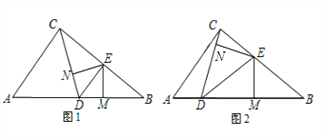
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D在边AB上运动,DE平分∠CDB交边BC于点E,EM⊥BD垂足为M,EN⊥CD垂足为N.
(1)当AD=CD时,求证:DE∥AC;
(2)探究:AD为何值时,△BME与△CNE相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级二班在订购本班的班服前,按身高型号进行登记,对女生的记录中,身高150cm以下记为S号,150160cm以下记为M号,160170cm以下记为L号.170cm 以上记为XL号.若用统计图描述这些数据,合适的统计图是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式不能运用平方差公式计算的是( )
A.(﹣x﹣y)(﹣x+y)
B.(﹣x+y)(x﹣y)
C.(x+y)(x﹣y)
D.(y+x)(x﹣y)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com