
【题目】如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( ) 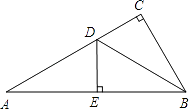
A.9cm
B.6cm
C.12cm
D.3cm
【答案】A
【解析】解:∵BD是∠ABC的平分线,∠C=90°,DE⊥AB, ∴DC=DE=3cm;
∵∠C=90°,∠A=30°,
∴∠ABC=90°﹣30°=60°,
∵BD是∠ABC的平分线,
∴∠DBE=∠CBD=60°÷2=30°,
∴BD=2DC=2×3=6(cm),
又∵∠A=30°,
∴∠A=∠DBE,
∴△ABD是等腰三角形,
∴AD=BD=6(cm),
∴AC=AD+DC=6+3=9(cm).
故选:A.
【考点精析】关于本题考查的角平分线的性质定理和含30度角的直角三角形,需要了解定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能得出正确答案.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】若点P是第二象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是( )
A.(﹣4,3)
B.(4,﹣3)
C.(﹣3,4)
D.(3,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
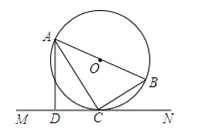
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.
(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD=30°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
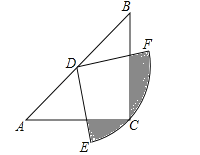
A.由小到大 B.由大到小 C.不变 D.先由小到大,后由大到小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,∠AOB、∠COD都是直角.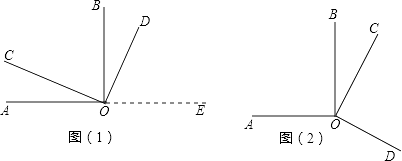
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com