
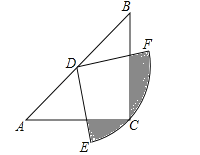
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
A.由小到大 B.由大到小 C.不变 D.先由小到大,后由大到小
【答案】C.
【解析】
试题分析:作DM⊥AC于M,DN⊥BC于N,连接DC,∵CA=CB,∠ACB=90°,∴∠A=∠B=45°,DM=![]() AD=
AD=![]() AB,DN=
AB,DN=![]() BD=
BD=![]() AB,∴DM=DN,∴四边形DNCN是正方形,∴∠MDN=90°,∴∠MDG=90°﹣∠GDN,∵∠EDF=90°,∴∠NDH=90°﹣∠GDN,∴∠MDG=∠NDH,在△DMG和△DNH中,∵∠MDG=∠NDH,∠DMG=∠DNH,DM=DH,∴△DMG≌△DNH,∴四边形DGCH的面积=正方形DMCN的面积,∵正方形DMCN的面积=
AB,∴DM=DN,∴四边形DNCN是正方形,∴∠MDN=90°,∴∠MDG=90°﹣∠GDN,∵∠EDF=90°,∴∠NDH=90°﹣∠GDN,∴∠MDG=∠NDH,在△DMG和△DNH中,∵∠MDG=∠NDH,∠DMG=∠DNH,DM=DH,∴△DMG≌△DNH,∴四边形DGCH的面积=正方形DMCN的面积,∵正方形DMCN的面积=![]() ,∴四边形DGCH的面积=
,∴四边形DGCH的面积=![]() ,∵扇形FDE的面积=
,∵扇形FDE的面积=![]() =
=![]() ,∴阴影部分的面积=扇形面积﹣四边形DGCH的面积=
,∴阴影部分的面积=扇形面积﹣四边形DGCH的面积=![]() (定值),故选C.
(定值),故选C.


科目:初中数学 来源: 题型:
【题目】某次数学趣味竞赛共有10道题目,每道题答对得10分,答错或不答得0分,全班40名同学参加了此次竞赛,他们的得分情况如下表所示
成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 |
人数 | 2 | 5 | 13 | 10 | 7 | 3 |
则全班40名同学的成绩的中位数和众数分别是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于换季,一家服装店的老板想将某服装打折销售,于是她和正在上七年级的儿子商量打折方案,下面是她和儿子商量时的对话情景:
妈妈:“儿子,每件衣服按标价的5折出售,可以吗?”
儿子:“若每件衣服按标价的5折出售会亏本30元.”
妈妈:“那每件衣服按标价的8折出售呢?”
儿子:“若每件衣服按标价的8折出售将会赚60元.”
……
请根据上面的信息,解决问题:
(1)求这种服装的标价.
(2)若要不亏本,至少打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( ) 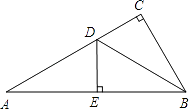
A.9cm
B.6cm
C.12cm
D.3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论:①△BDF、△CEF都是等腰三角形; ②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.其中正确的是( ) 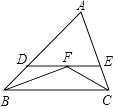
A.③④
B.①②
C.①②③
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.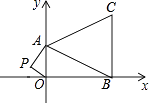
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
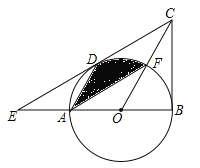
【题目】如图,在△BCE中,点A时边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
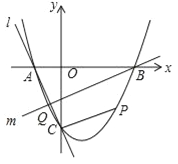
【题目】如图,抛物线![]() 与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3).
与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3).
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com