
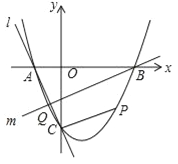
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬B������Ϊ��3��0������y�ύ�ڵ�C��0����3����
��x�ύ��A��B���㣬B������Ϊ��3��0������y�ύ�ڵ�C��0����3����
��1���������ߵĽ���ʽ��
��2����P��������λ�ڵ������IJ������˶������ı���ABPC��������ʱ�����P��������ı���ABPC����������
��3��ֱ��l����A��C���㣬��Q��������λ��y�����IJ������˶���ֱ��m������B�͵�Q���Ƿ����ֱ��m��ʹ��ֱ��l��m��x��Χ�ɵ������κ�ֱ��l��m��y��Χ�ɵ����������ƣ������ڣ����ֱ��m�Ľ���ʽ���������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��P������Ϊ��
����2��P��������![]() ��
��![]() ��ʱ���ı���ABPC��������������Ϊ
��ʱ���ı���ABPC��������������Ϊ![]() ����3�����ڣ�
����3�����ڣ�![]() ��
��
��������
��1����B��C����������������߽���ʽ�ɵ���![]() �������
�������![]() ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2��
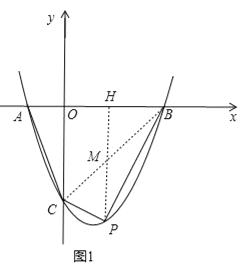
��ͼ1������BC����Py���ƽ���ߣ���BC�ڵ�M����x���ڵ�H����![]() �У���y=0�ɵ�
�У���y=0�ɵ�![]() �����x=��1��x=3����A������Ϊ����1��0������AB=3������1��=4����OC=3����S��ABC=
�����x=��1��x=3����A����������1��0������AB=3������1��=4����OC=3����S��ABC=![]() ABOC=
ABOC=![]() ��4��3=6����B��3��0����C��0����3������ֱ��BC����ʽΪy=x��3����P������Ϊ��x��
��4��3=6����B��3��0����C��0����3������ֱ��BC����ʽΪy=x��3����P������Ϊ��x��![]() ������M������Ϊ��x��x��3������P���ڵ����ޣ���PM=
������M������Ϊ��x��x��3������P���ڵ����ޣ���PM=![]() =
=![]() ����S��PBC=
����S��PBC=![]() PMOH+
PMOH+![]() PMHB=
PMHB=![]() PM��OH+HB��=
PM��OH+HB��=![]() PMOB=
PMOB=![]() PM���൱PM�����ֵʱ����PBC�����������ı���ABPC��������PM=
PM���൱PM�����ֵʱ����PBC�����������ı���ABPC��������PM=![]() =
=![]() ���൱x=
���൱x=![]() ʱ��PMmax=
ʱ��PMmax=![]() ����S��PBC=
����S��PBC=![]() =
=![]() ����ʱP������Ϊ��
����ʱP������Ϊ��![]() ��
��![]() ����S�ı���ABPC=S��ABC+S��PBC=6+
����S�ı���ABPC=S��ABC+S��PBC=6+![]() =
=![]() ������P��������
������P��������![]() ��
��![]() ��ʱ���ı���ABPC��������������Ϊ
��ʱ���ı���ABPC��������������Ϊ![]() ��
��
��3����ͼ2����ֱ��m��y���ڵ�N����ֱ��l�ڵ�G�����AGP=��GNC+��GCN������AGB�͡�NGC����ʱ�����С�AGB=��CGB���֡�AGB+��CGB=180�㣬���AGB=��CGB=90�㣬���ACO=��OBN����Rt��AON��Rt��NOB�����ߡ�AOC=��NOB��OC=OB����ACO=��NBO����Rt��AON��Rt��NOB��ASA������ON=OA=1����N������Ϊ��0����1������ֱ��m����ʽΪy=kx+d����B��N�����������ɵ�![]() �������
�������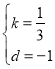 ����ֱ��m����ʽΪ
����ֱ��m����ʽΪ![]() ������������������ֱ��m�������ʽΪ
������������������ֱ��m�������ʽΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�CA=CB����ACB=90�㣬��AB���е�DΪԲ�ģ���Բ�Ľ�Ϊ90�������DEF����Cǡ��EF�ϣ����BDF=����0�㣼����90�㣩��������С����仯ʱ��ͼ����Ӱ���ֵ������ ��
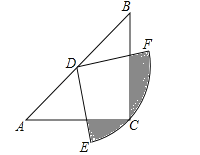
A����С���� B���ɴ�С C������ D������С�����ɴ�С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����ʾ����AOB����COD����ֱ�ǣ�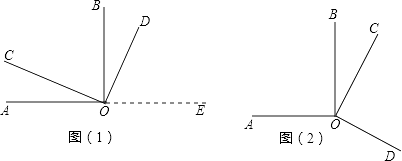
��1���Բ����AOD���COB������������ȣ����࣬���ǻ����Ĺ�ϵ�������������ķ���˵����IJ����Ǻ����ģ�
��2������COD���ŵ�O��ת��ͼ��2����ʾλ��ʱ�����ڣ�1���еIJ��뻹����������֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
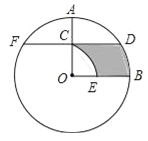
����Ŀ����ͼ���ڡ�O�У��뾶OA��OB������OA���е�C��FD��OB����O��D��F���㣬��CD=![]() ����OΪԲ�ģ�OCΪ�뾶��
����OΪԲ�ģ�OCΪ�뾶��![]() ����OB��E�㣮
����OB��E�㣮
��1�����O�İ뾶OA�ij���
��2��������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒԭ�ۼ�200Ԫ�����ڲ�Ʒ���������������ν��۴�������72Ԫ���ۼ����ۣ���֪���ν��۵İٷ�����ͬ�����轵�۵İٷ���Ϊx������г�����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У�����������ǣ�������
A.�����Խ�����ȵ��ı����Ǿ���
B.�����Խ����ഹֱ���ı���������
C.�����Խ�����ƽ�ֵ��ı�����ƽ���ı���
D.�����Խ����ഹֱ����ȵ��ı�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
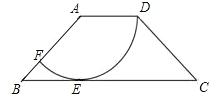
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��AD=2��AB=![]() ���Ե�AΪԲ�ģ�ADΪ�뾶��Բ��BC�����ڵ�E����AB�ڵ�F��
���Ե�AΪԲ�ģ�ADΪ�뾶��Բ��BC�����ڵ�E����AB�ڵ�F��
��1������ABE�Ĵ�С��![]() �ij��ȣ�
�ij��ȣ�
��2����BE���ӳ�����ȡһ��G��ʹ��![]() �ϵ�һ������P����G����̾���Ϊ
�ϵ�һ������P����G����̾���Ϊ![]() ����BG�ij���
����BG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.2a��a=2
B.m6��m2=m3
C.x2010+x2010=2x2010
D.t2��t3=t6
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com