
【题目】如图,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论:①△BDF、△CEF都是等腰三角形; ②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.其中正确的是( ) 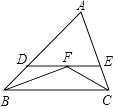
A.③④
B.①②
C.①②③
D.②③④
【答案】C
【解析】解:∵DE∥BC, ∴∠DFB=∠FBC,∠EFC=∠FCB,
∵△ABC中,∠ABC与∠ACB的平分线交于点F,
∴∠DBF=∠FBC,∠ECF=∠FCB,
∴∠DBF=∠DFB,∠ECF=∠EFC,
∴DB=DF,EF=EC,
即△BDF和△CEF都是等腰三角形;
故①正确;
∴DE=DF+EF=BD+CE,
故②正确;
∴△ADE的周长为:AD+DE+AE=AB+BD+CE+AE=AB+AC;
故③正确;
∵∠ABC不一定等于∠ACB,
∴∠FBC不一定等于∠FCB,
∴BF与CF不一定相等,
∴BD与CE不一定相等,故④错误.
故选C.
【考点精析】利用平行线的性质对题目进行判断即可得到答案,需要熟知两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:
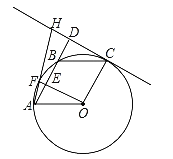
【题目】如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)若DH=![]() ,求EF和半径OA的长.
,求EF和半径OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
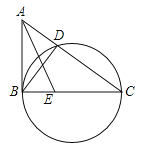
【题目】如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB.
(1)求证:AB是圆的切线;
(2)若点E是BC上一点,已知BE=4,tan∠AEB=![]() ,AB:BC=2:3,求圆的直径.
,AB:BC=2:3,求圆的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
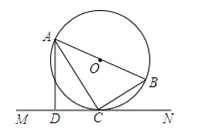
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.
(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD=30°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
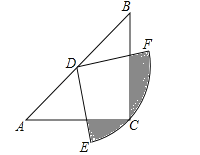
A.由小到大 B.由大到小 C.不变 D.先由小到大,后由大到小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() (m>0)与x轴的交点为A,B.
(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
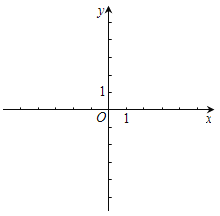
查看答案和解析>>
科目:初中数学 来源: 题型:
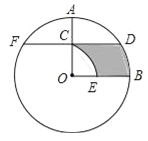
【题目】如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.
,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com