
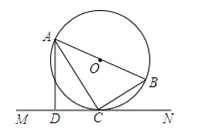
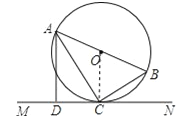
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.
(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD=30°,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,推出AD∥OC,推出OC⊥MN,根据切线的判定推出即可;
(2)求出AD、AC长,证△ADC∽△ACB,得出比例式,代入求出AB长即可.
试题解析:(1)证明:连接OC,因为OA=OC,所以∠BAC=∠ACO.因为AC平分∠BAD,所以∠BAC=∠CAD,故∠ACO=∠CAD.所以OC∥AD,又已知AD丄MN,所以OC丄MN,所以,直线MN是⊙O的切线;
(2)解:已知AB是⊙O的直径,则∠ACB=90°,又AD丄MN,则∠ADC=90°.因为CD=3,∠CAD=30°,所以AD=![]() ,AB=6.在Rt△ABC和Rt△ACD中,∠BAC=∠CAD,所以Rt△ABC∽Rt△ACD,则
,AB=6.在Rt△ABC和Rt△ACD中,∠BAC=∠CAD,所以Rt△ABC∽Rt△ACD,则![]() ,则AB=
,则AB=![]() ,所以⊙O的半径为
,所以⊙O的半径为![]() .
.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
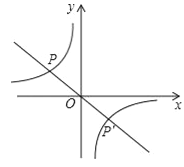
【题目】如图,点P(﹣3,1)是反比例函数![]() 的图象上的一点.
的图象上的一点.
(1)求该反比例函数的解析式;
(2)设直线y=kx与双曲线![]() 的两个交点分别为P和P′,当
的两个交点分别为P和P′,当![]() <kx时,直接写出x的取值范围.
<kx时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于换季,一家服装店的老板想将某服装打折销售,于是她和正在上七年级的儿子商量打折方案,下面是她和儿子商量时的对话情景:
妈妈:“儿子,每件衣服按标价的5折出售,可以吗?”
儿子:“若每件衣服按标价的5折出售会亏本30元.”
妈妈:“那每件衣服按标价的8折出售呢?”
儿子:“若每件衣服按标价的8折出售将会赚60元.”
……
请根据上面的信息,解决问题:
(1)求这种服装的标价.
(2)若要不亏本,至少打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
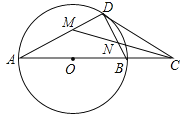
【题目】如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.
(1)求证:∠A=∠BDC;
(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( ) 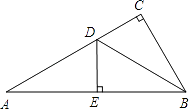
A.9cm
B.6cm
C.12cm
D.3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论:①△BDF、△CEF都是等腰三角形; ②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.其中正确的是( ) 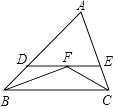
A.③④
B.①②
C.①②③
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.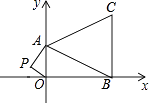
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com