
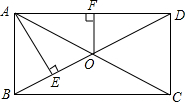
 如图,在矩形ABCD中,AE⊥BD于点E,BE=OE,过两条对角线的交点O作OF⊥AD,且OF=2,求BD的长.
如图,在矩形ABCD中,AE⊥BD于点E,BE=OE,过两条对角线的交点O作OF⊥AD,且OF=2,求BD的长. 分析 根据矩形的对角线相等且互相平分可得OA=OB=OD由线段垂直平分线的性质得出AB=OA,得出AB=OB=OA,由等腰三角形的性质得出AF=DF,证出OE是△AOD的中位线,根据三角形的中位线定理求出AB,得出OB,即可求出BD的长.
解答 解:∵四边形ABCD是矩形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OB=OD,
∵AE⊥BD于点E,BE=OE,
∴AB=OA,
∴OA=AB=OB,
∴OA=AB,
∵OF⊥AD,OF=2,
∴AF=DF,
∴OF是△ABD的中位线,
∴AB=2OF=2×2=4,
∴OB=4,
∴BD=2OB=2AB=2×4=8.
点评 本题考查了矩形的性质,三角形的中位线定理,线段垂直平分线的性质,等腰三角形的性质;熟练掌握矩形的性质,证出AB=OB和OF是△ABD的中位线是解决问题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:选择题
| A. | 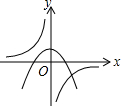 | B. | 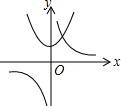 | C. |  | D. | 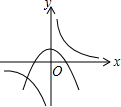 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
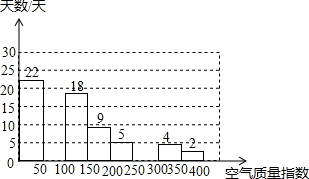 为了解空气质量情况,河北省某市从环境检测网随机抽取了2015年100天的空气质量指数,绘制了如图所示的统计表和如图所示的不完整的频数分布直方图,请你根据图表中提供的信息,解答下面的问题.
为了解空气质量情况,河北省某市从环境检测网随机抽取了2015年100天的空气质量指数,绘制了如图所示的统计表和如图所示的不完整的频数分布直方图,请你根据图表中提供的信息,解答下面的问题. | 级别 | 空气质量指数 | 天数 |
| 优 | 0-50 | 22 |
| 良 | 51-100 | m |
| 轻度污染 | 101-150 | 18 |
| 中度污染 | 151-200 | 9 |
| 重度污染 | 201-300 | 15 |
| 严重污染 | 301-400 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
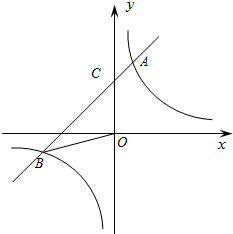 如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:m、n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图象经过点A(-m,0)、B(0,n).
已知:m、n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图象经过点A(-m,0)、B(0,n).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线l∥x轴,分别与函数$y=\frac{2}{x}$(x>0)和$y=\frac{k}{x}$(x<0)的图象相交于点A、B,交y轴于点C,若AC=2BC,则k=-1.
如图,直线l∥x轴,分别与函数$y=\frac{2}{x}$(x>0)和$y=\frac{k}{x}$(x<0)的图象相交于点A、B,交y轴于点C,若AC=2BC,则k=-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com