
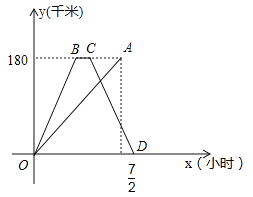
【题目】快、慢两车分别从相距180 km的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() h,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(km)与所用时间x(h)的函数图象如图所示,请结合图象信息解答下列问题:
h,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(km)与所用时间x(h)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(km)与x(h)的函数关系式;
(3)两车出发后经过多长时间相距90 km的路程?直接写出答案.

【答案】(1)快车速度: 120千米/时,慢车速度:60千米/时;(2)y=﹣120x+420(2≤x≤![]() );(3)两车出发后经过
);(3)两车出发后经过![]() 或
或![]() 或
或![]() 小时相距90千米的路程.
小时相距90千米的路程.
【解析】
试题(1)根据路程与相应的时间,求得快车与慢车的速度;
(2)先求得点C的坐标,再根据点D的坐标,运用待定系数法求得CD的解析式;
(3)分三种情况:在两车相遇之前;在两车相遇之后;在快车返回之后,分别求得时间即可.
试题解析:解:(1)快车速度:180×2÷(![]() )=120千米/时,慢车速度:120÷2=60千米/时;
)=120千米/时,慢车速度:120÷2=60千米/时;
(2)快车停留的时间:![]() =
=![]() (小时),
(小时),![]() =2(小时),即C(2,180),设CD的解析式为:y=kx+b,则
=2(小时),即C(2,180),设CD的解析式为:y=kx+b,则
将C(2,180),D(![]() ,0)代入,得:
,0)代入,得: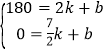 ,解得:
,解得:![]() ,∴快车返回过程中y(千米)与x(小时)的函数关系式为y=﹣120x+420(2≤x≤
,∴快车返回过程中y(千米)与x(小时)的函数关系式为y=﹣120x+420(2≤x≤![]() );
);
(3)相遇之前:120x+60x+90=180,解得x=![]() ;
;
相遇之后:120x+60x﹣90=180,解得x=![]() ;
;
快车从甲地到乙地需要180÷120=![]() 小时,快车返回之后:60x=90+120(x﹣
小时,快车返回之后:60x=90+120(x﹣![]() ﹣
﹣![]() ),解得x=
),解得x=![]() .
.
综上所述,两车出发后经过![]() 或
或![]() 或
或![]() 小时相距90千米的路程.
小时相距90千米的路程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 与y轴交于点A.
与y轴交于点A.
(1)如图,直线![]() 与直线
与直线![]() 交于点B,与y轴交于点C,点B横坐标为
交于点B,与y轴交于点C,点B横坐标为![]() .
.
①求点B的坐标及k的值;
②直线![]() 与直线
与直线![]() 与y轴所围成的△ABC的面积等于 ;
与y轴所围成的△ABC的面积等于 ;
(2)直线![]() 与x轴交于点E(
与x轴交于点E(![]() ,0),若
,0),若![]() ,求k的取值范围.
,求k的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).
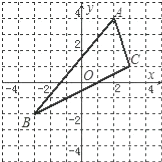
(1)在图中画出△ABC关于y轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在某市五个区投放共享单车供市民使用,投放量的分布及投放后的使用情况统计如下. 
(1)该公司在全市一共投放了万辆共享单车;
(2)在扇形统计图中,B区所对应扇形的圆心角为°;
(3)该公司在全市投放的共享单车的使用量占投放量的85%,请计算C区共享单车的使用量并补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,点D、E分别在AC、BC上,且CDBC=ACCE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB、BC分别交于点F、G. 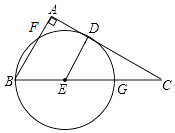
(1)求证:AC是⊙E的切线.
(2)若AF=4,CG=5,求⊙E的半径;
(3)若Rt△ABC的内切圆圆心为I,则IE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读材料,再尝试解决问题:
完全平方式![]() 以及
以及![]() 的值为非负数的特点在数学学习中有广泛的应用,比如探求
的值为非负数的特点在数学学习中有广泛的应用,比如探求![]() 的最大(小)值时,我们可以这样处理:
的最大(小)值时,我们可以这样处理:
解:原式 = ![]() .
.
因为无论![]() 取什么数,都有
取什么数,都有![]() 的值为非负数,所以
的值为非负数,所以![]() 的最小值为0;此时
的最小值为0;此时![]() 时,进而
时,进而![]() 的最小值是
的最小值是![]() ;所以当
;所以当![]() 时,原多项式的最小值是
时,原多项式的最小值是![]() .
.
请根据上面的解题思路,探求:
⑴.多项式![]() 的最小值是多少,并写出对应的
的最小值是多少,并写出对应的![]() 的取值;
的取值;
⑵.多项式![]() 的最大值是多少,并写出对应的
的最大值是多少,并写出对应的![]() 的取值.
的取值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com