
【题目】如图,在Rt△ABC中,∠A=90°,点D、E分别在AC、BC上,且CDBC=ACCE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB、BC分别交于点F、G. 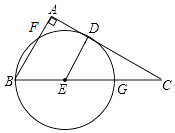
(1)求证:AC是⊙E的切线.
(2)若AF=4,CG=5,求⊙E的半径;
(3)若Rt△ABC的内切圆圆心为I,则IE= .
【答案】
(1)证明:∵CDBC=ACCE,
∴ ![]() ,
,
∵∠DCE=∠ACB,
∴△CDE∽△CAB,
∴∠EDC=∠A=90°,
∴ED⊥AC,
∵点D在⊙E上,
∴AC是⊙E的切线
(2)①如图1,
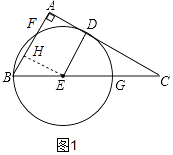
过E作EH⊥AB于H,
∴BH=FH,
∵∠A=∠AHE=∠ADE=90°,
∴四边形AHED是矩形,
∴ED=AH,ED∥AB,
∴∠B=∠DEC,
设⊙E的半径为r,则EB=ED=EG=r,
∴BH=FH=AH﹣AF=DE﹣AF=r﹣4,
EC=EG+CG=r+5,
在△BHE和△EDC中,
∵∠B=∠DEC,∠BHE=∠EDC=90°,
∴△BHE∽△EDC,
∴ ![]() ,即
,即 ![]() ,
,
∴r=20,
∴⊙E的半径为20
(3)![]()
【解析】如图2 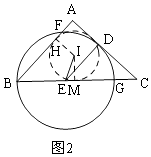
过I作IM⊥BC于M,过I作IH⊥AB于H,
由(2)得:FH=BH=r﹣4=20﹣4=16,AB=AF+2BH=4+2×16=36,
BC=2r+5=2×20+5=45,
∴AC= ![]() =27,
=27,
∵I是Rt△ABC的内心,
∴IM= ![]() =
= ![]() =9,
=9,
∴AH=IM=9,
∴BH=BM=36﹣9=27,
∴EM=27﹣20=7,
在Rt△IME中,由勾股定理得:IE= ![]() =
= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了等腰直角三角形和三角形的内切圆与内心的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】快、慢两车分别从相距180 km的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() h,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(km)与所用时间x(h)的函数图象如图所示,请结合图象信息解答下列问题:
h,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(km)与所用时间x(h)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(km)与x(h)的函数关系式;
(3)两车出发后经过多长时间相距90 km的路程?直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家用1200元购进了一批T恤,上市后很快售完,商家又用2800元购进了第二批这种T恤,所购数量是第一批购进量的2倍,但单价贵了5元.
(1)该商家购进的第一批T恤是多少件?
(2)若两批T恤按相同的标价销售,最后剩下20件按八折优惠卖出,如果希望两批T恤全部售完的利润率不低于16%(不考虑其它因素),那么每件T恤的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经学习过反比例函数y= ![]() 的图象和性质,请回顾研究它的过程,对函数y=
的图象和性质,请回顾研究它的过程,对函数y= ![]() 进行探索.下列结论:
进行探索.下列结论:
①图象在第一、二象限,②图象在第一、三象限,
③图象关于y轴对称,④图象关于原点对称,
⑤当x>0时,y随x增大而增大;当x<0时,y随x增大而增大,
⑥当x>0时,y随x增大而减小;当x<0时,y随x增大而增大,
是函数y= ![]() 的性质及它的图象特征的是: . (填写所有正确答案的序号)
的性质及它的图象特征的是: . (填写所有正确答案的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,AB∥CD,AC,BD交于O点,过O点的直线EF交AD于E点,交BC于F点,且BF=DE,则图中的全等三角形共有( )

A. 6对 B. 5对 C. 3对 D. 2对
查看答案和解析>>
科目:初中数学 来源: 题型:
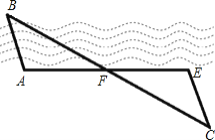
【题目】如图,小明和小月两家位于A,B两处隔河相望,要测得两家之间的距离,小明设计方案如下:
①从点A出发沿河岸画一条射线AM;
②在射线AM上截取AF=FE;
③过点E作EC∥AB,使B,F,C在一条直线上;
④CE的长就是A,B间的距离.
(1)请你说明小明设计的原理.
(2)如果不借助测量仪,小明的设计中哪一步难以实现?
(3)你能设计出更好的方案吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com