
【题目】在平面直角坐标系xOy中,直线![]() 与y轴交于点A.
与y轴交于点A.
(1)如图,直线![]() 与直线
与直线![]() 交于点B,与y轴交于点C,点B横坐标为
交于点B,与y轴交于点C,点B横坐标为![]() .
.
①求点B的坐标及k的值;
②直线![]() 与直线
与直线![]() 与y轴所围成的△ABC的面积等于 ;
与y轴所围成的△ABC的面积等于 ;
(2)直线![]() 与x轴交于点E(
与x轴交于点E(![]() ,0),若
,0),若![]() ,求k的取值范围.
,求k的取值范围.

【答案】(1)①(-1,3),1;②![]() ;(2)2<k<4.
;(2)2<k<4.
【解析】
试题(1)①将x=-1代入y=-2x+1,得出B点坐标,进而求出k的值;
②求出A,C点坐标,进而得出AC的长,即可得出△ABC的面积:
∵k=1,∴一次函数解析式为:y="x+4." ∴A(0,4).
∵y=-2x+1,∴C(0,1).∴AC=4-1=3.
∴△ABC的面积为:![]() ×1×3=
×1×3=![]() .
.
(2)分别得出当x0=-2以及-1时k的值,进而得出k的取值范围.
试题解析:解:(1)①∵直线y=-2x+1过点B,点B的横坐标为-1,∴y=2+2=3.
∴B(-1,3).
∵直线y=kx+4过B点,
∴3=-k+4,解得:k=1.
②![]() .
.
(2)∵直线y=kx+4(k≠0)与x轴交于点E(x0,0),![]() ,
,
∴当x0=-2,则E(-2,0),代入y=kx+4得:0=-2k+4,解得:k=2.
当x0=-1,则E(-1,0),代入y=kx+4得:0=-k+4,解得:k=4.
∴k的取值范围是:2<k<4.


科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,下列条件中,不能说明AB⊥CD的是( )

A. ∠AOD=90°
B. ∠AOC=∠BOC
C. ∠BOC+∠BOD=180°
D. ∠AOC+∠BOD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1). 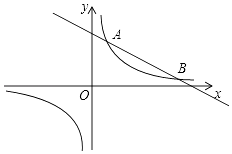
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
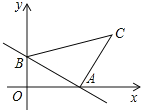
【题目】如图,一次函数y=﹣![]() x+3的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,则过B、C两点直线的解析式是_____.
x+3的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,则过B、C两点直线的解析式是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
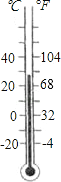
【题目】温度与我们的生活息息相关,你仔细观察过温度计吗?如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(℉),设摄氏温度为x(℃),华氏温度为y(℉),则y是x的一次函数.
(1)仔细观察图中数据,试求出y与x之间的函数表达式;
(2)当摄氏温度为零下15℃时,求华氏温度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快、慢两车分别从相距180 km的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() h,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(km)与所用时间x(h)的函数图象如图所示,请结合图象信息解答下列问题:
h,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(km)与所用时间x(h)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(km)与x(h)的函数关系式;
(3)两车出发后经过多长时间相距90 km的路程?直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?(要有必要的过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com