
| 金额(元) | 20 | 30 | 35 | 50 | 100 |
| 学生数(人) | 3 | 7 | 5 | 15 | 10 |
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
| 3 |
| A、5个 | B、6个 | C、7个 | D、8个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
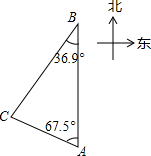 某国汉阳石油运输船在临近我国海域发生原油泄漏事故,我国国家海洋局紧急调集海上巡逻的海监船,在相关海域进行现场监测与海洋采样,如图,上午9时,海监船位于A处,观测到某还港口城市P位于海监船的北偏西67.5°方向,海监船以21海里/时的速度向正北方向行驶,下午2时海监船到达B处,这时观察到城市P位于海监船的南偏西36.9°,求此时海监船所在B处于城市P的距离?
某国汉阳石油运输船在临近我国海域发生原油泄漏事故,我国国家海洋局紧急调集海上巡逻的海监船,在相关海域进行现场监测与海洋采样,如图,上午9时,海监船位于A处,观测到某还港口城市P位于海监船的北偏西67.5°方向,海监船以21海里/时的速度向正北方向行驶,下午2时海监船到达B处,这时观察到城市P位于海监船的南偏西36.9°,求此时海监船所在B处于城市P的距离?| 3 |
| 5 |
| 3 |
| 4 |
| 12 |
| 13 |
| 12 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 5 |
| 3 |
| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
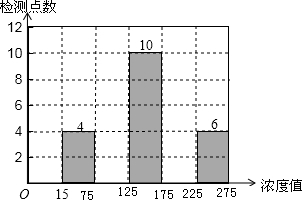 我国PM2.5标准:日平均浓度小于75微克/立方米为安全值.根据某市40个国控监测点某日PM2.5监测数据,绘制成如下所示的频数分布表.
我国PM2.5标准:日平均浓度小于75微克/立方米为安全值.根据某市40个国控监测点某日PM2.5监测数据,绘制成如下所示的频数分布表.| 组别 | PM2.5(微克/立方米)日平均浓度值分组 | 频数 | 频率 |
| 1 | 25~75 | 4 | 0.1 |
| 2 | 75~125 | a | 0.2 |
| 3 | 125~175 | 10 | 0.25 |
| 4 | 175~225 | b | c |
| 5 | 225~275 | 6 | 0.15 |
| 合计 | 以上分组均含最小值 不含最大值 | 40 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在矩形ABCD中,对角线AC、BD相交于G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△EFD,其中相似的为( )
如图,在矩形ABCD中,对角线AC、BD相交于G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△EFD,其中相似的为( )| A、①④ | B、①② |
| C、②③④ | D、①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com