
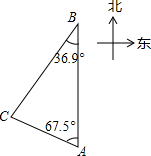
 某国汉阳石油运输船在临近我国海域发生原油泄漏事故,我国国家海洋局紧急调集海上巡逻的海监船,在相关海域进行现场监测与海洋采样,如图,上午9时,海监船位于A处,观测到某还港口城市P位于海监船的北偏西67.5°方向,海监船以21海里/时的速度向正北方向行驶,下午2时海监船到达B处,这时观察到城市P位于海监船的南偏西36.9°,求此时海监船所在B处于城市P的距离?
某国汉阳石油运输船在临近我国海域发生原油泄漏事故,我国国家海洋局紧急调集海上巡逻的海监船,在相关海域进行现场监测与海洋采样,如图,上午9时,海监船位于A处,观测到某还港口城市P位于海监船的北偏西67.5°方向,海监船以21海里/时的速度向正北方向行驶,下午2时海监船到达B处,这时观察到城市P位于海监船的南偏西36.9°,求此时海监船所在B处于城市P的距离?| 3 |
| 5 |
| 3 |
| 4 |
| 12 |
| 13 |
| 12 |
| 5 |
| x |
| tan36.9° |
| x |
| tan67.5° |
| x |
| tan36.9° |
| x |
| tan67.5° |
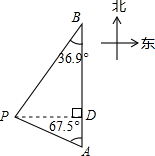 解:过P作PD⊥AB,垂足为D,
解:过P作PD⊥AB,垂足为D,| x |
| BD |
| x |
| tan36.9° |
| x |
| tan67.5° |
| x |
| tan36.9° |
| x |
| tan67.5° |
| PD |
| BP |
| PD |
| sin36.9° |


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
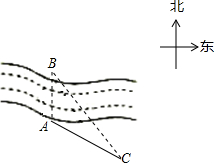 在一次测量活动中,同学们想测量河岸上的树A与它对岸正北方向的树B之间的距离,如图,他们在河岸边上选择了与树A及树B在同一水平面上的点C的北偏西35°方向,树A位于点C的北偏西58°方向,又测得A、C间的距离为100m,请你利用以上测得的数据求出树A 树B之间的距离.(结果精确到1米,参考数据sin23°≈0.391,sin35°≈0.574,tan35°≈0.700,sin58°≈0.848,cos58°≈0.530.)
在一次测量活动中,同学们想测量河岸上的树A与它对岸正北方向的树B之间的距离,如图,他们在河岸边上选择了与树A及树B在同一水平面上的点C的北偏西35°方向,树A位于点C的北偏西58°方向,又测得A、C间的距离为100m,请你利用以上测得的数据求出树A 树B之间的距离.(结果精确到1米,参考数据sin23°≈0.391,sin35°≈0.574,tan35°≈0.700,sin58°≈0.848,cos58°≈0.530.)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一段抛物线:y=-x(x-4)(0≤x≤4),记为C1,它与x轴交于点O,A1;将C2绕点A2;…如此进行下去,得到一条连续的曲线,若P(2013,m)在这条曲线上,则m的值为( )
如图,一段抛物线:y=-x(x-4)(0≤x≤4),记为C1,它与x轴交于点O,A1;将C2绕点A2;…如此进行下去,得到一条连续的曲线,若P(2013,m)在这条曲线上,则m的值为( )| A、4 | B、3 | C、-4 | D、-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
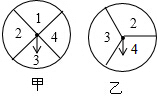 在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,当同时转动甲、乙两个转盘,停止后指针所指的两个数字x,y分别表示两条线段的长,已知第三条线段的长为5,如果将转盘转动停止后得到的三条线段长记为(x,y,5).
在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,当同时转动甲、乙两个转盘,停止后指针所指的两个数字x,y分别表示两条线段的长,已知第三条线段的长为5,如果将转盘转动停止后得到的三条线段长记为(x,y,5).查看答案和解析>>
科目:初中数学 来源: 题型:
| 金额(元) | 20 | 30 | 35 | 50 | 100 |
| 学生数(人) | 3 | 7 | 5 | 15 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com