
| 2 |
| 5 |
| 3 |
| 10 |
| 2 |
| 5 |
| 3 |
| 10 |
| 3 |
| 10 |
| 1 |
| 9 |
| 7 |
| 27 |
| 2 |
| 5 |
| 3 |
| 10 |
| 3 |
| 10 |
| 2 |
| 5 |


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
 如图,AB是⊙O的直径,BC⊥AB,连接OC交⊙O于E点,弦AD∥OC,弦DF⊥AB于点G.
如图,AB是⊙O的直径,BC⊥AB,连接OC交⊙O于E点,弦AD∥OC,弦DF⊥AB于点G.| 4 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
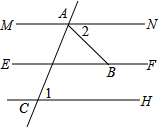 推理填空:如图,MN/EF,GH∥EF,∠CAB=68°,∠1=70°,求∠ABE的度数
推理填空:如图,MN/EF,GH∥EF,∠CAB=68°,∠1=70°,求∠ABE的度数查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一段抛物线:y=-x(x-4)(0≤x≤4),记为C1,它与x轴交于点O,A1;将C2绕点A2;…如此进行下去,得到一条连续的曲线,若P(2013,m)在这条曲线上,则m的值为( )
如图,一段抛物线:y=-x(x-4)(0≤x≤4),记为C1,它与x轴交于点O,A1;将C2绕点A2;…如此进行下去,得到一条连续的曲线,若P(2013,m)在这条曲线上,则m的值为( )| A、4 | B、3 | C、-4 | D、-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 金额(元) | 20 | 30 | 35 | 50 | 100 |
| 学生数(人) | 3 | 7 | 5 | 15 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
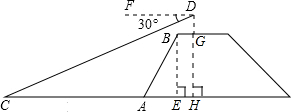 如图,张明站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,他测得小船C的俯角是∠FDC=30°,若张明的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,tan∠BAE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:根号
如图,张明站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,他测得小船C的俯角是∠FDC=30°,若张明的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,tan∠BAE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:根号| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com