
【题目】如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H. 
(1)求证:△EAB≌△GAD;
(2)若AB=3 ![]() ,AG=3,求EB的长.
,AG=3,求EB的长.
【答案】
(1)证明:∵四边形ABCD、AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG,
∴∠EAB=∠GAD,
在△AEB和△AGD中,
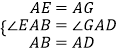 ,
,
∴△EAB≌△GAD(SAS)
(2)证明:∵△EAB≌△GAD,
∴EB=GD,
∵四边形ABCD是正方形,AB=3 ![]() ,
,
∴BD⊥AC,AC=BD= ![]() AB=6,
AB=6,
∴∠DOG=90°,OA=OD= ![]() BD=3,
BD=3,
∵AG=3,
∴OG=OA+AG=6,
∴GD= ![]() =3
=3 ![]() ,
,
∴EB=3 ![]() .
.
【解析】(1)由四边形ABCD、AGFE是正方形,即可得AB=AD,AE=AG,∠DAB=∠EAG,然后利用SAS即可证得△EAB≌△GAD,(2)由(1)则可得EB=GD,然后在Rt△ODG中,利用勾股定理即可求得GD的长,继而可得EB的长.
【考点精析】根据题目的已知条件,利用正方形的性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列6个代数式:ab、ac、a+b+c、2a+b、2a﹣b中,其值为正的式子的个数是( ) 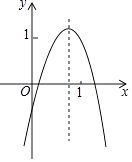
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次时装表演会预算中票价定为每张100元,容纳观众人数不超过2000人,毛利润y(百元)关于观众人数x(百人)之间的函数图象如图所示,当观众人数超过1000人时,表演会组织者需向保险公司缴纳定额平安保险5000(不列入成本费用),请解答下列问题: 
(1)当观众不超过1000人时,毛利润y关于观众人数x的函数解析式和成本费用s(百元)关于观众人数x(百人)的函数解析式;
(2)若要使这次表演会获得36000元的毛利润,那么需售出多少张门票需支付成本费用多少元(当观众人数不超过1000人时,表演会的毛利润=门票收入﹣成本费用;当观众人数超过1000人时,表演会的毛利润=门票收入﹣成本费用﹣平安保险费).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证).
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1 , 再以正方形的对角线OA2作正方形OA1A2B1 , …,依此规律,则点A8的坐标是( )
A.(﹣8,0)
B.(0,8)
C.(0,8 ![]() )
)
D.(0,16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年6月份,我市某果农收获荔枝30吨,香蕉13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往深圳,已知甲种货车可装荔枝4吨和香蕉1吨,乙种货车可装荔枝香蕉各2吨; 
(1)该果农安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(2)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1300元,则该果农应选择哪种方案使运费最少,最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH= ![]() BD
BD
其中正确结论的为(请将所有正确的序号都填上).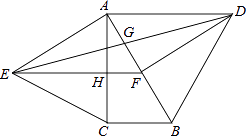
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中: ①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S= ![]() ACBD.
ACBD.
正确的是(填写所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com