
����Ŀ��һ��ʱװ���ݻ�Ԥ����Ʊ�۶�Ϊÿ��100Ԫ�����ɹ�������������2000�ˣ�ë����y����Ԫ�����ڹ�������x�����ˣ�֮��ĺ���ͼ����ͼ��ʾ����������������1000��ʱ�����ݻ���֯�������չ�˾���ɶ���ƽ������5000��������ɱ����ã��������������⣺ 
��1�������ڲ�����1000��ʱ��ë����y���ڹ�������x�ĺ�������ʽ�ͳɱ�����s����Ԫ�����ڹ�������x�����ˣ��ĺ�������ʽ��
��2����Ҫʹ��α��ݻ���36000Ԫ��ë������ô���۳���������Ʊ��֧���ɱ����ö���Ԫ������������������1000��ʱ�����ݻ��ë����=��Ʊ���멁�ɱ����ã���������������1000��ʱ�����ݻ��ë����=��Ʊ���멁�ɱ����é�ƽ�����շѣ���
���𰸡�
��1���⣺����ͼ֪����0��x��10��10��x��20ʱ��y����x��һ�κ�����
��0��x��10ʱ����y����x�ĺ�������ʽΪy=kx+b��
�ѵ㣨0����100������10��400�����뺯������ʽ���ã�
![]() ��
��
��ã� ![]() ��
��
����y=50x��100��0��x��10����
��S=100x����50x��100��=50x+100��0��x��10��
��2���⣺��0��x��10ʱ�������⣬֪50x��100=360��
����x=9.2��S=50x+100=50��9.2+100=560��
��10��x��2 0ʱ����y=mx+n��
�ѵ㣨10��350����20��850�����뺯������ʽ��
�� ![]() ��
��
��ã� ![]() ��
��
����y=50x��150��10��x��20����
S=100x����50x��150����50=50x+100 ��10��x��20����
��y=360ʱ��50x��150=360�����x=10.2��
����S=50��10.2+100=610��
��������Ʊ920�Ż�1020�ţ���Ӧ����֧���ɱ����÷ֱ�Ϊ56000Ԫ��61000Ԫ
����������1���ɸ��ݴ���ϵ������ȷ������ʽ����2�����ݣ�1���к����������Լ��Ա�����ȡֵ��Χ���жϳ���ͬ�����µIJ�ͬ�������


 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬABCD�У�AB=5��BC=3���Ȱ�ͼ��2��������������ֽƬABCD�ع���A��ֱ���۵���ʹ��D���ڱ�AB�ϵĵ�E�����ۺ�ΪAF���ٰ�ͼ��3���������ع���F��ֱ���۵���ʹ��C����EF�ϵĵ�H�����ۺ�ΪFG����A��H�����ľ���Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����CD�ǡ�O��һ���ң���CD��AB�ڵ�E��CD=4 ![]() ��AE=2�����O�İ뾶Ϊ ��
��AE=2�����O�İ뾶Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=3ax2+2bx+c
��1����a=b=1��c=��1�����������x��Ľ������ꣻ
��2����a= ![]() ��c=2+b���������ک�2��x��2�����ϵ���Сֵ�ǩ�3����b��ֵ��
��c=2+b���������ک�2��x��2�����ϵ���Сֵ�ǩ�3����b��ֵ��
��3����a+b+c=1���Ƿ����ʵ��x��ʹ����Ӧ��y��ֵΪ1����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=3��AC=4��BC=5��PΪ��BC��һ���㣬PE��AB��E��PF��AC��F��MΪEF�е㣬��AM����СֵΪ�� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱߡ�ABC�ı߳���2��D��E�ֱ�ΪAB��AC���е㣬�ӳ�BC����F��ʹCF= ![]() BC������CD��EF��
BC������CD��EF�� 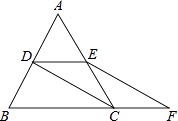
��1����֤��DE=CF��
��2����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y= ![]() ��ͼ����һ�κ���y=mx+b��ͼ����A��1��3����B��n����1�����㣮
��ͼ����һ�κ���y=mx+b��ͼ����A��1��3����B��n����1�����㣮 
��1������������һ�κ����ĺ�����ϵʽ��
��2�����AOB�������
��3������֪����һ�κ���y=x��1��ͼ�����������������y=x��ͼ������ƽ��1�����ȵ�λ�õ����Խ��ƽ�ƽ���������⣺�ڣ�1���������£�������̽����
�ٺ���y= ![]() ��ͼ�������y=
��ͼ�������y= ![]() ��ͼ��������ƽ�Ƶõ���
��ͼ��������ƽ�Ƶõ���
�ڵ�P��x1 �� y1����Q ��x2 �� y2�� �ں���y= ![]() ��ͼ���ϣ�x1��x2 �� �ԱȽ�y1��y2�Ĵ�С��
��ͼ���ϣ�x1��x2 �� �ԱȽ�y1��y2�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����G��������ABCD�Խ���CA���ӳ���������һ�㣬���߶�AGΪ����һ��������AEFG���߶�EB��GD�ཻ�ڵ�H�� 
��1����֤����EAB�ա�GAD��
��2����AB=3 ![]() ��AG=3����EB�ij���
��AG=3����EB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��������y���ϣ���C������Ϊ��2��0������B�������ǣ�0��2����ֱ��AC�Ľ���ʽΪ ![]() ����tanA��ֵ�� ��
����tanA��ֵ�� �� 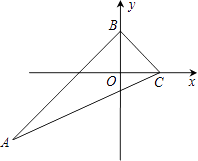
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com