
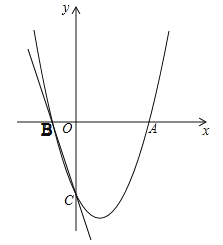
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).
(1)求该抛物线的解析式;
(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;
(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)M(﹣![]() ,﹣
,﹣![]() );(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,P的坐标为(1+
);(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,P的坐标为(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)或(2,﹣3).
,3)或(2,﹣3).
【解析】
(1)把A,B,C的坐标代入抛物线解析式求出a,b,c的值即可;
(2)由题意得到直线BC与直线AM垂直,求出直线BC解析式,确定出直线AM中k的值,利用待定系数法求出直线AM解析式,联立求出M坐标即可;
(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,分两种情况,利用平移规律确定出P的坐标即可.
(1)把A(3,0),B(﹣1,0),C(0,﹣3)代入抛物线解析式得: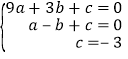 ,
,
解得: ,
,
则该抛物线解析式为y=x2﹣2x﹣3;
(2)设直线BC解析式为y=kx﹣3,
把B(﹣1,0)代入得:﹣k﹣3=0,即k=﹣3,
∴直线BC解析式为y=﹣3x﹣3,
∴直线AM解析式为y=![]() x+m,
x+m,
把A(3,0)代入得:1+m=0,即m=﹣1,
∴直线AM解析式为y=![]() x﹣1,
x﹣1,
联立得: ,
,
解得: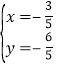 ,
,
则M(﹣![]() ,﹣
,﹣![]() );
);
(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,
分两种情况考虑:
设Q(x,0),P(m,m2﹣2m﹣3),
当四边形BCQP为平行四边形时,由B(﹣1,0),C(0,﹣3),
根据平移规律得:﹣1+x=0+m,0+0=﹣3+m2﹣2m﹣3,
解得:m=1±![]() ,x=2±
,x=2±![]() ,
,
当m=1+![]() 时,m2﹣2m﹣3=8+2
时,m2﹣2m﹣3=8+2![]() ﹣2﹣2
﹣2﹣2![]() ﹣3=3,即P(1+
﹣3=3,即P(1+![]() ,3);
,3);
当m=1﹣![]() 时,m2﹣2m﹣3=8﹣2
时,m2﹣2m﹣3=8﹣2![]() ﹣2+2
﹣2+2![]() ﹣3=3,即P(1﹣
﹣3=3,即P(1﹣![]() ,3);
,3);
当四边形BCPQ为平行四边形时,由B(﹣1,0),C(0,﹣3),
根据平移规律得:﹣1+m=0+x,0+m2﹣2m﹣3=﹣3+0,
解得:m=0或2,
当m=0时,P(0,﹣3)(舍去);当m=2时,P(2,﹣3),
综上,存在以点B,C,Q,P为顶点的四边形是平行四边形,P的坐标为(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)或(2,﹣3).
,3)或(2,﹣3).


科目:初中数学 来源: 题型:
【题目】某商场出售一批进价为2元的贺卡,在营运中发现此商品的日销价x(单位:元)与销售量y(单位:张)之间有如下关系:
x/元 | 3 | 4 | 5 | 6 |
y/张 | 20 | 15 | 12 | 10 |
(1)猜测并确定y与x的函数关系式.
(2)当日销售单价为10元时,贺卡的日销售量是多少张?
(3)设此卡的利润为W元,试求出W与x之间的函数关系式,若物价部门规定此卡的销售单价不能超过10元,试求出当日销售单价为多少元时,每天获得的利润最大并求出最大的利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y= -3x+6的图象与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点.
两点.
(1)将直线![]() 向左平移1个单位长度,求平移后直线的函数关系式;
向左平移1个单位长度,求平移后直线的函数关系式;
(2)求出平移过程中,直线![]() 在第一象限扫过的图形的面积.
在第一象限扫过的图形的面积.
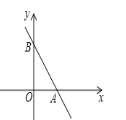
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
∵![]() =
=![]() ×
×![]() ,
,![]() =
=![]() ×
×![]() ,
,![]() =
=![]() ×
×![]() ,…,
,…,![]() =
=![]() ×
×![]() ,
,
∴![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ×
×![]() +
+![]() ×
×![]() +
+![]() ×
×![]() +…+
+…+![]() ×
×![]()
=![]() ×
×![]() =
=![]() ×
×![]() =
=![]() .
.
请解答下列问题:
(1)在和式![]() +
+![]() +
+![]() +…中,第100项是 ;
+…中,第100项是 ;
(2)化简![]() +
+![]() +
+![]() +…+
+…+![]() ,并求n=100时分式的值;
,并求n=100时分式的值;
(3)根据上面的方法,解方程:![]() +
+![]() +
+![]() =
=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
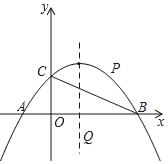
【题目】如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;
(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
数学活动课上,老师准备了若干个如图![]() 的三种纸片,
的三种纸片,![]() 种纸片边长为
种纸片边长为![]() 的正方形,
的正方形,![]() 种纸片是边长为
种纸片是边长为![]() 的正方形,
的正方形,![]() 种纸片长为
种纸片长为![]() 、宽为
、宽为![]() 的长方形,并用
的长方形,并用![]() 种纸片一张,
种纸片一张,![]() 种纸片一张,
种纸片一张,![]() 种纸片两张拼成如图
种纸片两张拼成如图![]() 的大正方形.
的大正方形.

(1)请用两种不同的方法求图![]() 大正方形的面积.
大正方形的面积.
方法1:__________________________;
方法2:__________________________.
(2)观察图![]() ,请你写出下列三个代数式:
,请你写出下列三个代数式:![]() ,
,![]() ,
,![]() 之间的等量关系_____________________.
之间的等量关系_____________________.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,
,![]() ,求
,求![]() 的值;
的值;
②已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及D点的坐标;
(3)二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
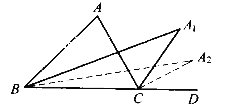
【题目】如图,在![]() ABC中,
ABC中, ![]() A=80
A=80![]() ,
, ![]() ABC与
ABC与![]() ACD的平分线交于点A1,得
ACD的平分线交于点A1,得![]() A1;
A1; ![]() A1BC与
A1BC与![]() A1CD的平分线相交于点A2,得
A1CD的平分线相交于点A2,得![]() A2;……;
A2;……; ![]() A7BC与
A7BC与![]() A7CD的平分线相交于点A8,得
A7CD的平分线相交于点A8,得![]() A8,则
A8,则![]() A8的度数为()
A8的度数为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com