
【题目】乘法公式的探究及应用.
数学活动课上,老师准备了若干个如图![]() 的三种纸片,
的三种纸片,![]() 种纸片边长为
种纸片边长为![]() 的正方形,
的正方形,![]() 种纸片是边长为
种纸片是边长为![]() 的正方形,
的正方形,![]() 种纸片长为
种纸片长为![]() 、宽为
、宽为![]() 的长方形,并用
的长方形,并用![]() 种纸片一张,
种纸片一张,![]() 种纸片一张,
种纸片一张,![]() 种纸片两张拼成如图
种纸片两张拼成如图![]() 的大正方形.
的大正方形.

(1)请用两种不同的方法求图![]() 大正方形的面积.
大正方形的面积.
方法1:__________________________;
方法2:__________________________.
(2)观察图![]() ,请你写出下列三个代数式:
,请你写出下列三个代数式:![]() ,
,![]() ,
,![]() 之间的等量关系_____________________.
之间的等量关系_____________________.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,
,![]() ,求
,求![]() 的值;
的值;
②已知![]() ,求
,求![]() 的值.
的值.
【答案】(1)(a+b)2;a2+b2+2ab;(2)(a+b)2=a2+2ab+b2;(3)①ab=11;②(x-2019)2=16
【解析】
(1)方法1:图2是边长为a+b的正方形,利用正方形的面积公式可得出S正方形=(a+b)2;方法2:图2可看成1个边长为a的正方形、1个边长为b的正方形以及2个长为b宽为a的长方形的组合体,根据正方形及长方形的面积公式可得出S正方形=a2+2ab+b2;
(2)由图2中的图形面积不变,可得出(a+b)2=a2+2ab+b2;
(3)①由a+b=6可得出(a+b)2=36,即a2+b2+2ab=36,将a2+b2=14代入即可求出ab的值;
②设x-2018=a+1,则x-2019=a,x-2020=a-1,再根据完全平方公式求解即可.
解:(1)方法1:图2是边长为a+b的正方形,
∴S正方形=(a+b)2;
方法2:图2可看成1个边长为a的正方形、1个边长为b的正方形以及2个长为b宽为a的长方形的组合体,
∴S正方形=a2+b2+2ab.
(2)由图2中的图形面积不变,可得出(a+b)2=a2+2ab+b2;
(3)①∵a+b=6,
∴(a+b)2=36,即a2+b2+2ab=36,
又∵a2+b2=14,
∴14+2ab=36,
∴ab=11;
②设x-2019=a,则x-2018=a+1,x-2020=a-1,
∵(x-2018)2+(x-2020)2=34,
∴(a+1)2+(a-1)2=34,
∴a2+2a+1+a2-2a+1=20,
∴2a2+2=34,
∴2a2=32,
∴a2=16,
即(x-2019)2=16.


科目:初中数学 来源: 题型:
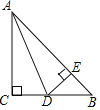
【题目】如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:AC=AE;
(2)若△BDE的周长为20,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
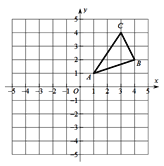
【题目】如图,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
.
(1)若![]() 与
与![]() 关于y轴成轴对称,则
关于y轴成轴对称,则![]() 三个顶点坐标分别为
三个顶点坐标分别为![]() _________,
_________,![]() ____________,
____________,![]() ____________;
____________;
(2)若P为x轴上一点,则![]() 的最小值为____________;
的最小值为____________;
(3)计算![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
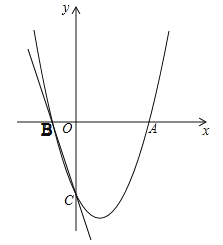
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).
(1)求该抛物线的解析式;
(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;
(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论:①abc<0 ②b2﹣4ac>0 ③4b+c<0 ④若B(﹣![]() ,y1)、C(﹣
,y1)、C(﹣![]() ,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
其中正确的结论是(填写代表正确结论的序号)__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
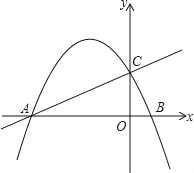
【题目】如图,已知直线y=![]() x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+4ax+b经过A、C两点,与x轴交于另一点B.
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+4ax+b经过A、C两点,与x轴交于另一点B.
(1)求抛物线的解析式:
(2)点Q在抛物线上,且S△AQC=S△BQC,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
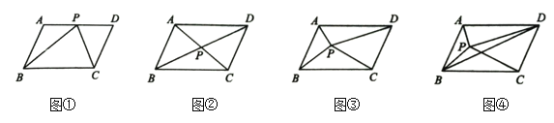
【题目】如图,四边形![]() 是面积为
是面积为![]() 的平行四边形,其中
的平行四边形,其中![]() .
.
(1)如图①,点![]() 为
为![]() 边上任意一点,则
边上任意一点,则![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系是__________;
之间的数量关系是__________;
(2)如图②,设![]() 交于点
交于点![]() ,则
,则![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系是___________;
之间的数量关系是___________;
(3)如图③,点![]() 为
为![]() 内任意一点时,试猜想
内任意一点时,试猜想![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(4)如图④,已知点![]() 为
为![]() 内任意一点,
内任意一点,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com