
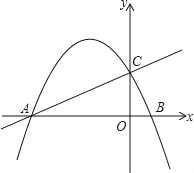
【题目】如图,已知直线y=![]() x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+4ax+b经过A、C两点,与x轴交于另一点B.
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+4ax+b经过A、C两点,与x轴交于另一点B.
(1)求抛物线的解析式:
(2)点Q在抛物线上,且S△AQC=S△BQC,求点Q的坐标.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+2;(2)Q(﹣4,2)或(﹣
x+2;(2)Q(﹣4,2)或(﹣![]() ,﹣
,﹣![]() ).
).
【解析】
(1)先求出A、C两点坐标,再利用待定系数法即可解决问题;(2)①分点Q在x轴上方时,根据平行线间的距离相等可得当CQ∥AB时,△AQC和△BQC面积相等,然后根据点Q与点C的纵坐标相等,利用抛物线解析式列式计算即可得解;②点Q在x轴下方时,设CQ与x轴相交于点D,根据△AQC和△BQC面积相等可知AD=BD,然后求出点D的坐标,再利用待定系数法求出直线CD的解析式,与抛物线联立求解即可得到点Q的坐标.
(1)∵当y=0时,则有![]() x+2=0,解得x=﹣5,
x+2=0,解得x=﹣5,
∴点A的坐标为(﹣5,0),
∵当x=0时,则有y=2,
∴点C的坐标为(0,2),
∵抛物线y=ax2+4ax+b经过A、C两点,把(0,2)(﹣5,0)代入得
∴![]() ,解得
,解得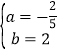 ,
,
∴抛物线为y=﹣![]() x2﹣
x2﹣![]() x+2.
x+2.
(2)①当Q在x轴上方时(如图1),
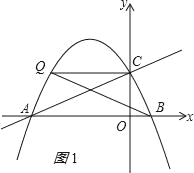
△ACQ和△BCQ同底,若它们的面积相等,则A、B到直线CQ的距离相等,即CQ∥AB;
∵抛物线的对称轴为x=﹣2,
∴点Q坐标为(﹣4,2);
②当Q在x轴下方时(如图2),
,设CQ与x轴交于点D,若△AQC和△BQC面积相等,则有AD=BD
令y=0,则﹣![]() x2﹣
x2﹣![]() x+2=0,解得x1=﹣5,x2=1,即AB=6
x+2=0,解得x1=﹣5,x2=1,即AB=6
∴点D的坐标为(﹣2,0)
设直线CD的解析式为y=kx+b,把(0,2)(﹣2,0)代入得
![]() 解得
解得![]() ,
,
∴直线CD的解析式为y=x+2,
∵点Q在直线CD与抛物线上,
∴x+2=﹣![]() x2﹣
x2﹣![]() x+2,解得x1=0,x2=﹣
x+2,解得x1=0,x2=﹣![]() ,
,
∴点Q坐标为(﹣![]() ,﹣
,﹣![]() );
);
∴点Q的坐标为(﹣4,2)或(﹣![]() ,﹣
,﹣![]() )
)


科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)-(3)题:数学课上,老师出示了这样一道题:如图1,点![]() 是正
是正![]() 边
边![]() 上一点以
上一点以![]() 为边做正
为边做正![]() ,连接
,连接![]() .探究线段
.探究线段![]() 与
与![]() 的数量关系,并证明.同学们经过思考后,交流了自已的想法:
的数量关系,并证明.同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 相等.”
相等.”
小伟:“通过全等三角形证明,再经过进一步推理,可以得到线段![]() 平分
平分![]() .”......
.”......
老师:“保留原题条件,连接![]() ,
,![]() 是
是![]() 的延长线上一点,
的延长线上一点,![]() (如图2),如果
(如图2),如果![]() ,可以求出
,可以求出![]() 、
、![]() 、
、![]() 三条线段之间的数量关系.”
三条线段之间的数量关系.”
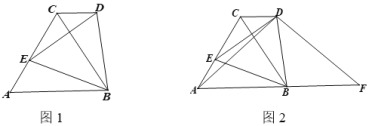
(1)求证![]() ;
;
(2)求证线段![]() 平分
平分![]() ;
;
(3)探究![]() 、
、![]() 、
、![]() 三条线段之间的数量关系,并加以证明.
三条线段之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
∵![]() =
=![]() ×
×![]() ,
,![]() =
=![]() ×
×![]() ,
,![]() =
=![]() ×
×![]() ,…,
,…,![]() =
=![]() ×
×![]() ,
,
∴![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ×
×![]() +
+![]() ×
×![]() +
+![]() ×
×![]() +…+
+…+![]() ×
×![]()
=![]() ×
×![]() =
=![]() ×
×![]() =
=![]() .
.
请解答下列问题:
(1)在和式![]() +
+![]() +
+![]() +…中,第100项是 ;
+…中,第100项是 ;
(2)化简![]() +
+![]() +
+![]() +…+
+…+![]() ,并求n=100时分式的值;
,并求n=100时分式的值;
(3)根据上面的方法,解方程:![]() +
+![]() +
+![]() =
=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
数学活动课上,老师准备了若干个如图![]() 的三种纸片,
的三种纸片,![]() 种纸片边长为
种纸片边长为![]() 的正方形,
的正方形,![]() 种纸片是边长为
种纸片是边长为![]() 的正方形,
的正方形,![]() 种纸片长为
种纸片长为![]() 、宽为
、宽为![]() 的长方形,并用
的长方形,并用![]() 种纸片一张,
种纸片一张,![]() 种纸片一张,
种纸片一张,![]() 种纸片两张拼成如图
种纸片两张拼成如图![]() 的大正方形.
的大正方形.

(1)请用两种不同的方法求图![]() 大正方形的面积.
大正方形的面积.
方法1:__________________________;
方法2:__________________________.
(2)观察图![]() ,请你写出下列三个代数式:
,请你写出下列三个代数式:![]() ,
,![]() ,
,![]() 之间的等量关系_____________________.
之间的等量关系_____________________.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,
,![]() ,求
,求![]() 的值;
的值;
②已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,乙从B地到A地需要( )分钟
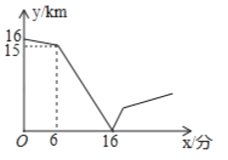
A.12B.14C.18D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及D点的坐标;
(3)二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
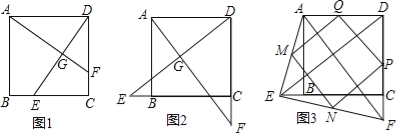
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如图两幅统计图(不完整).
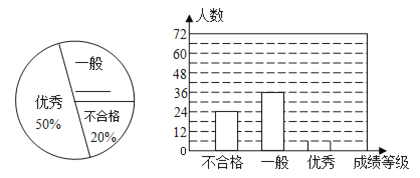
请你根据图中所给的信息解答下列问题:
(1)这次测试,一共抽取了名学生;
(2)请将以上两幅统计图补充完整;(注:扇形图补百分比,条形图补“优秀”人数与高度);
(3)若“一般”和“优秀”均被视为达标成绩,该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天猫店销售某种规格学生软式排球,成本为每个30元.以往销售大数据分析表明:当每只售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个,若售价每下降1元,其月销售量就增加200个.
(1)若售价上涨m元,每月能售出 个排球(用m的代数式表示).
(2)为迎接“双十一”,该天猫店在10月底备货1300个该规格的排球,并决定整个11月份进行降价促销,问售价定为多少元时,能使11月份这种规格排球获利恰好为8400元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com