
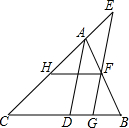
 如图,已知∠ADB+∠EGC=180°,AD平分∠BAC,HF∥BC.
如图,已知∠ADB+∠EGC=180°,AD平分∠BAC,HF∥BC.分析 (1)根据同旁内角互补,两直线平行,得出AD∥EG,再根据两直线平行同位角相,内错角相等得出∠CAD=∠E,∠DAB=∠AFE,最后根据角平分线的性质得出∠CAD=∠DAB,从而得出∠AFE=∠E;
(2)根据AD∥EG,得出∠ADB=∠EGB,再根据HF∥BC,得出∠HFG=∠EGB,从而得出∠ADB=∠HFG,再根据∠ADB=78°,即可得出∠HFG的度数.
解答 解:(1)∵∠ADB+∠EGC=180°,
∴AD∥EG,
∴∠CAD=∠E,∠DAB=∠AFE,
∵AD平分∠BAC,
∴∠CAD=∠DAB,
∴∠AFE=∠E;
(2)∵AD∥EG,
∴∠ADB=∠EGB,
∵HF∥BC,
∴∠HFG=∠EGB,
∴∠ADB=∠HFG,
∵∠ADB=78°,
∴∠HFG=78°.
点评 此题考查了平行线的判定与性质,用到的知识点为:同旁内角互补,两直线平行;两直线平行,内错角相等,同位角相等.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.17×106 | B. | 1.7×105 | C. | 1.7×106 | D. | 17×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
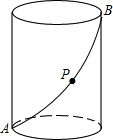 如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )
如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )| A. | 2$\sqrt{{π}^{2}+4}$cm | B. | 4$\sqrt{{π}^{2}+4}cm$ | C. | 8$\sqrt{{π}^{2}+4}cm$ | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | 1.5 | 3 | 4 | 9 | 16 | 24 |
| f(a) | 2x+y | $\frac{1+2x+y}{2}$ | 1-2x-y | 1+2x+y | 2-4x-2y | -2x-y |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
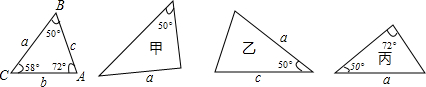
| A. | 只有乙 | B. | 只有丙 | C. | 甲和乙 | D. | 乙和丙 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com