
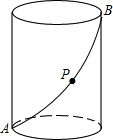
 如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )
如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )| A. | 2$\sqrt{{π}^{2}+4}$cm | B. | 4$\sqrt{{π}^{2}+4}cm$ | C. | 8$\sqrt{{π}^{2}+4}cm$ | D. | 无法确定 |
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:选择题
| A. | 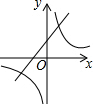 | B. | 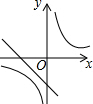 | C. | 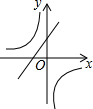 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
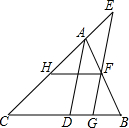 如图,已知∠ADB+∠EGC=180°,AD平分∠BAC,HF∥BC.
如图,已知∠ADB+∠EGC=180°,AD平分∠BAC,HF∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
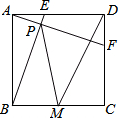 如图,正方形ABCD中,AB=4,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为2$\sqrt{10}$.
如图,正方形ABCD中,AB=4,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为2$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
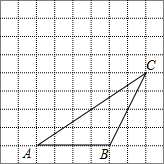 如下图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′、中线A′E.
如下图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′、中线A′E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5 | B. | 19-4k | C. | 13 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com