练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

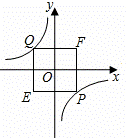
    如图，P、Q是反比例函数图象上两点，且关于原点对称，QE⊥x轴，矩形PEQF的面积是3，则反比例函数的表达式为__________．

     


    y=﹣．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    为了了解中学生参加体育活动情况，某校对部分学生进行了调查，其中一个问题是：“你平均每天参加体育活动的时间是多少？”共有4个选项（每个时间段含最小值不含最大值）：

    A．1.5小时以上     B．1﹣1.5小时   C．0.5﹣1小时     D．0.5小时以下

    根据调查结果绘制了两幅不完整的统计图．请你根据以上信息解答下列问题：

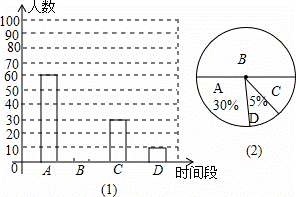
    （1）本次调查活动采取了__________的调查方式．（填“普查”或“抽样调查”）

    （2）本次调查共调查了__________人，图（2）中选项C的圆心角为__________度．

    （3）请将图（1）中选项B的部分补充完整．

    （4）若该校有2000名学生，你估计该校可能有__________名学生平均每天参加体育活动的时间在1小时以下．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若a为整数，则下列事件是随机事件的是(     )

        A．a2+2=0              B．a2＞0

        C．|a|是一个非负数     D．2a是偶数

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若点（2，6）是反比例函数y=图象上一点，则此函数图象必经过点(     )

          A．（3，4）           B．（3，﹣4）             C．（﹣4，3）             D．（4，﹣3）

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    当m=__________时，关于x的方程=2﹣无解．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：103+（）﹣2×（﹣600）0﹣（﹣3）3×0.1﹣1×π0

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


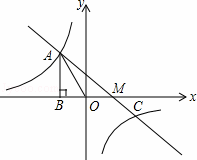
    已知反比例函数图象过第二象限内的点A（﹣2，m），作AB⊥x轴于点B，Rt△AOB面积为3．

    （1）求k和m的值；

    （2）若直线y=ax+b经过点A，并且经过反比例函数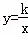的图象上另一点C（4，﹣）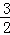

    ①求直线y=ax+b关系式；

    ②设直线y=ax+b与x轴交于M，求AM的长；

    ③根据图象写出使反比例函数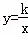值大于一次函数y=ax+b的值的x的取值范围．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知一次函数y=2x﹣b与两个坐标轴围成的三角形面积为9，则b=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    阅读材料：

    例：说明代数式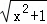+ 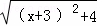的几何意义，并求它的最小值．

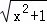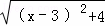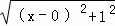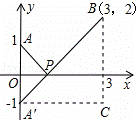
    解：+=+，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则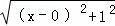可以看成点P与点A（0，1）的距离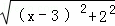，可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA+PB的最小值．

    设点A关于x轴的对称点为A′，则PA=PA′，因此，求PA+PB的最小值，只需求PA′+PB的最小值，而点A′、B间的直线段距离最短，所以PA′+PB的最小值为线段A′B的长度．为此，构造直角三角形A′CB，因为A′C=3，CB=3，所以A′B=3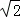，即原式的最小值为3．

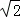    根据以上阅读材料，解答下列问题：

    （1）代数式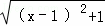+的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B（2，3）或（2，﹣3）的距离之和．（填写点B的坐标）

    （2）代数式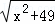+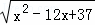的最小值．

    　

    查看答案和解析>>

    同步练习册答案