

分析 (1)利用矩形的性质得出y=-$\sqrt{3}$x+b必经过线段OB的中点,即可确定出b;
(2)先利用角平分线的性质求出OG,再确定出OM即可得出点M坐标,即可得出结论;
(3)设出平移后的直线解析式,先确定出O'H=OC=2$\sqrt{3}$,从而确定出n,即可得出结论.
解答 解:(1)∵四边形OABC为矩形,点A、C的坐标分别为(4,0),(0,2$\sqrt{3}$),
∴B(4,2$\sqrt{3}$),
∴OB的中点坐标为(2,$\sqrt{3}$)
∵直线y=-$\sqrt{3}$x+b平分矩形OABC的面积,
∴直线y=-$\sqrt{3}$x+b必经过线段OB的中点,
∴$\sqrt{3}$=-$\sqrt{3}$×2+b,
∴b=3$\sqrt{3}$,
(2)如图1,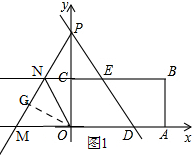
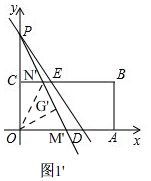
当直线y=-$\sqrt{3}$x+b绕点P顺时针旋转和x轴负半轴相较于M,(如图1),
当直线y=-$\sqrt{3}$x+b绕点P顺时针旋转和x轴正半轴相较于M,(如图1'),
过点O作OG⊥PM,
∵C(0,2$\sqrt{3}$),
∴OC=2$\sqrt{3}$,
∵ON平分∠CNM,且OC⊥BC,OG⊥NM,
∴OG=OC=2$\sqrt{3}$,
由(1)知,点P(0,3$\sqrt{3}$),
∴OP=3$\sqrt{3}$,
∴sin∠OPM=$\frac{OG}{OP}$=$\frac{2\sqrt{3}}{3\sqrt{3}}$=$\frac{2}{3}$,
在Rt△POM中,设OM=2a,则PM=3a,
∵OP=3$\sqrt{3}$,根据勾股定理得,PM2=OM2+OP2,
即:9a2=4a2+27,
∴a=-$\frac{3\sqrt{15}}{5}$(舍)或a=$\frac{3\sqrt{15}}{5}$,
∴OM=2a=$\frac{6\sqrt{15}}{5}$,
∴M(-$\frac{6\sqrt{15}}{5}$,0)或M($\frac{6\sqrt{15}}{5}$,0),
∵直线PE解析式为y=-$\sqrt{3}$x+3$\sqrt{3}$,
∴D(3,0),
∴DM=$\frac{6\sqrt{15}}{5}-3$或DM=3+$\frac{6\sqrt{15}}{5}$.
(3)如图2,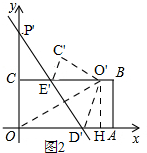
假设沿DE折叠点O落不在边BC上,那么直线DE向右平移n个单位点O刚好落在边BC上的点O',得到直线D'E',
∵直线DE解析式为y=-$\sqrt{3}$x+3$\sqrt{3}$,则直线D'E'解析式为y=-$\sqrt{3}$(x-n)+3$\sqrt{3}$,∠P'D'O=∠PDO=60°,
由折叠有,∠P'D'O'=∠P'D'O=60°,
∴∠O'D'H=60°,
过点O'作O'H⊥OA,
∵点O'在边BC上,
∴O'H=OC=2$\sqrt{3}$,
在Rt△O'D'H中,O'D'=$\frac{O'H}{sin∠O'D'H}$=$\frac{2\sqrt{3}}{sin60°}$=4,
由折叠得,O'D'=OD'=4,
∴D'(4,0),
∴n=1,
∴直线D'E'解析式为y=-$\sqrt{3}$x+4$\sqrt{3}$,
∴直线DE和直线D'E'解析式不一样,
∴矩形OABC沿DE折叠,点O没落在边BC上,而沿直线D'E'解析式为y=-$\sqrt{3}$x+4$\sqrt{3}$折叠,点O落在了边CB的延长线上.
即:沿直线D'E'解析式为y=-$\sqrt{3}$x+4$\sqrt{3}$折叠,点O落在了边CB的延长线上.
点评 此题是一次函数综合题,主要考查了矩形的性质,锐角三角函数,勾股定理,角平分线的性质,平移的性质,解本题的关键是求出DM.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:解答题
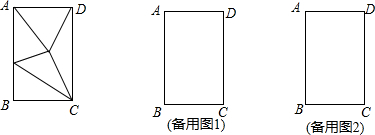
 按要求画出图形:如图,△AOB是等腰直角三角形,∠AOB=90°,OA=OB,请你在图中画出以点O为中心,将△AOE逆时针旋转90°之后的图形.(不写傲法.写出结论)
按要求画出图形:如图,△AOB是等腰直角三角形,∠AOB=90°,OA=OB,请你在图中画出以点O为中心,将△AOE逆时针旋转90°之后的图形.(不写傲法.写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,反比例函数y=$\frac{16}{x}$在第一象限内的图象经过点A,与BC交于点F,OB=3$\sqrt{3}$,BF=$\frac{1}{2}$BC.过点F作EF∥OB,交OA于点,点P为直线EF上的一个动点,连接PA,PO,若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标.
如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,反比例函数y=$\frac{16}{x}$在第一象限内的图象经过点A,与BC交于点F,OB=3$\sqrt{3}$,BF=$\frac{1}{2}$BC.过点F作EF∥OB,交OA于点,点P为直线EF上的一个动点,连接PA,PO,若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com