
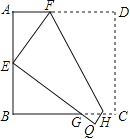
【题目】如图,将边长为6的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在点Q处,EQ与BC交于点G,则△EBG的周长是 cm.
【答案】12
【解析】
试题根据翻折的性质可得DF=EF,设EF=x,表示出AF,然后利用勾股定理列方程求出x,从而得到AF、EF的长,再求出△AEF和△BGE相似,根据相似三角形对应边成比例列式求出BG、EG,然后根据三角形周长的定义列式计算即可得解.
解:由翻折的性质得,DF=EF,
设EF=x,则AF=6﹣x,
∵点E是AB的中点,
∴AE=BE=![]() ×6=3,
×6=3,
在Rt△AEF中,AE2+AF2=EF2,
即32+(6﹣x)2=x2,
解得x=![]() ,
,
∴AF=6﹣![]() =
=![]() ,
,
∵∠FEG=∠D=90°,
∴∠AEF+∠BEG=90°,
∵∠AEF+∠AFE=90°,
∴∠AFE=∠BEG,
又∵∠A=∠B=90°,
∴△AEF∽△BGE,
∴![]() =
=![]() =
=![]() ,
,
即![]() =
=![]() =
=![]() ,
,
解得BG=4,EG=5,
∴△EBG的周长=3+4+5=12.
故答案为12.


科目:初中数学 来源: 题型:
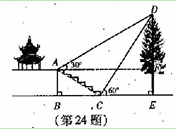
【题目】(本题7分)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为![]() (即AB:BC=
(即AB:BC=![]() ),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:我们学习过直角三角形斜边上的中线等于斜边的一半,即:如图1,在![]() 中,
中,![]() ,若点
,若点![]() 是斜边
是斜边![]() 的中点,则
的中点,则![]()
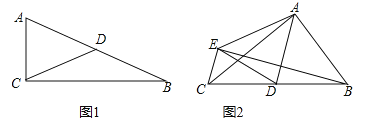
灵活应用:如图2,![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() 连接
连接![]() .
.
(1)线段![]() 的长是 ;
的长是 ;
(2)判断![]() 的形状并说明理由;
的形状并说明理由;
(3)线段![]() 的长是 .
的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
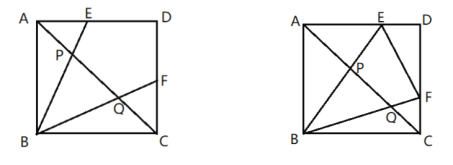
【题目】如图正方形![]() 的顶点
的顶点![]() 是
是![]() 和
和![]() 上的动点,与
上的动点,与![]() 交于P、Q两点,
交于P、Q两点,![]() .
.
(1)当![]() 时,
时,
①求![]() 的度数;
的度数;
②求以![]() 为边长的正方形面积;
为边长的正方形面积;
(2)当![]() 在
在![]() 上运动时,始终保持
上运动时,始终保持![]() ,连接
,连接![]() ,则
,则![]() 面积的最小值为 (直接写出答案).
面积的最小值为 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() 是
是![]() 边上的一点,
边上的一点,![]() ,
,![]() 是
是![]() 的外接圆,
的外接圆,![]() 是
是![]() 的直径,且交
的直径,且交![]() 于点
于点![]() .
.
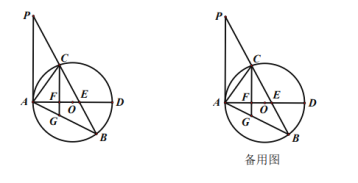
(1)求证: ![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() 若
若![]() 求
求![]() 的长;
的长;
(3)在满足(2)的条件下,若![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.

(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON及其边上一点A,以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C,再以点C为圆心,AC长为半径画弧,恰好经过点B,错误的结论是( ).
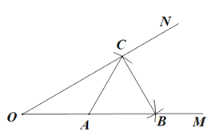
A.![]() B.∠OCB=90°C.∠MON=30°D.OC=2BC
B.∠OCB=90°C.∠MON=30°D.OC=2BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育看台侧面的示意图如图所示,观众区AC的坡度i为1:2,顶端C离水平地面AB的高度为10m,从顶棚的D处看E处的仰角α=18°30′,竖直的立杆上C、D两点间的距离为4m,E处到观众区底端A处的水平距离AF为3m.
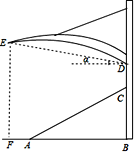
求:(1)观众区的水平宽度AB;
(2)顶棚的E处离地面的高度EF.(sin18°30′≈0.32,tanl8°30′≈0.33,结果精确到0.1m)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com