
【题目】如图正方形![]() 的顶点
的顶点![]() 是
是![]() 和
和![]() 上的动点,与
上的动点,与![]() 交于P、Q两点,
交于P、Q两点,![]() .
.
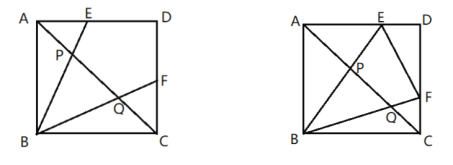
(1)当![]() 时,
时,
①求![]() 的度数;
的度数;
②求以![]() 为边长的正方形面积;
为边长的正方形面积;
(2)当![]() 在
在![]() 上运动时,始终保持
上运动时,始终保持![]() ,连接
,连接![]() ,则
,则![]() 面积的最小值为 (直接写出答案).
面积的最小值为 (直接写出答案).
【答案】(1)①![]() ,②以
,②以![]() 为边的正方形面积为
为边的正方形面积为![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据正方形性质得出![]() ,
,![]() ,由此得知
,由此得知![]() ,然后根据AB=AQ=CP,结合等腰三角形性质以及三角形内角和定理进一步求出答案即可;
,然后根据AB=AQ=CP,结合等腰三角形性质以及三角形内角和定理进一步求出答案即可;
(2)首先根据勾股定理求出![]() ,由此得出
,由此得出![]() ,通过证明
,通过证明![]() 进一步得出
进一步得出![]() ,据此即可得出答案;
,据此即可得出答案;
(3)延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,先证明
,先证明![]() 与
与![]() 全等,得出∠GBF=∠EBF,再证明
全等,得出∠GBF=∠EBF,再证明![]() 与
与![]() 全等,从而得出
全等,从而得出![]() ,即当
,即当![]() 时,
时,![]() 取得最小值,设此时
取得最小值,设此时![]() ,则
,则![]() ,根据题意利用勾股定理得出
,根据题意利用勾股定理得出![]() ,最后得出
,最后得出![]() ,
,![]() ,据此进一步求解即可.
,据此进一步求解即可.
(1)①∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵AB=AQ=CP,
∴AB=AQ=CP=BC,
∴![]() ,
,
同理![]() ,
,
∴![]() ;
;
②∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
故以![]() 为边的正方形面积为
为边的正方形面积为![]() ;
;
(2)如图,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,
,
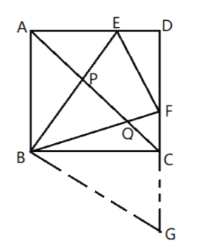
在![]() 与
与![]() 中,
中,
∵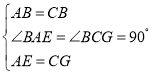
∴![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴∠GBF=∠EBF,
在![]() 与
与![]() 中,
中,
∵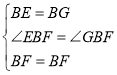
∴![]()
∴![]() ,
,
在![]() 中,
中,![]() ,
,
当且仅当![]() 时等号成立,此时
时等号成立,此时![]() ,
,
设此时![]() ,则
,则![]() ,
,
![]()
由![]() 得:
得:![]()
即![]()
解得![]() (舍去),
(舍去),
∴![]() ,
,![]() ,
,
∴![]() 面积的最小值=
面积的最小值=![]() ,
,
故答案为:![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】有红、黄两个布袋,红布袋中有两个完全相同的小球,分别标有数字2和4.黄布袋中有三个完全相同的小球,分别标有数字﹣2,﹣4和﹣6.小贤先从红布袋中随机取出一个小球,记录其标有的数字为x,再从黄布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点M的一个坐标为(x.y)
(1)用列表或画树状图的方法写出点M的所有可能坐标;
(2)求点M落在双曲线y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
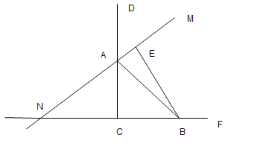
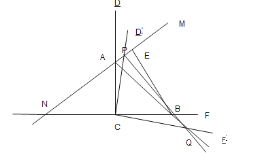
【题目】如图,在![]() 中,
中,![]() 是
是![]() 外角
外角![]() 的角平分线,反向延长
的角平分线,反向延长![]() 与线段
与线段![]() 延长线交于点
延长线交于点![]() 过
过![]() 作
作![]() 于点
于点![]() 将
将![]() 旋转,得到
旋转,得到![]() 为
为![]() 与
与![]() 的交点,
的交点,![]() 为
为![]() 与
与![]() 延长线的交点,现有以下结论:
延长线的交点,现有以下结论:
![]() ;
;
![]() 若
若![]() ;
;
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若
若![]() 且
且![]() 时,
时,![]() .
.
其中正确的结论是_____________________(填写所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
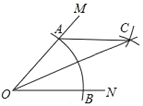
【题目】如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
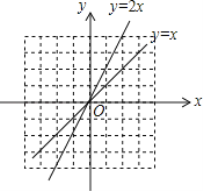
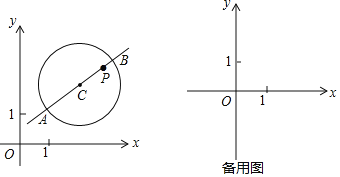
【题目】在平面直角坐标系xOy中,⊙C的半径为r(r>1),P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:若直线CP与⊙C交于点A,B,满足|PA﹣PB|=2,则称点P为⊙C的“完美点”,如图为⊙C及其“完美点”P的示意图.
(1)当⊙O的半径为2时,
①在点M![]() ,N(0,1),T
,N(0,1),T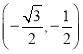 中,⊙O的“完美点”是 ;
中,⊙O的“完美点”是 ;
②若⊙O的“完美点”P在直线y=![]() x上,求PO的长及点P的坐标;
x上,求PO的长及点P的坐标;
(2)⊙C的圆心在直线y=![]() x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求篮板底部支架HE与支架AF所成的∠FHE的度数.
(2)求篮板底部点E到地面的距离,(精确到0.01米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
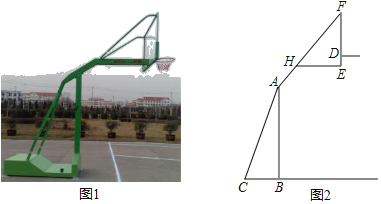
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为6的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在点Q处,EQ与BC交于点G,则△EBG的周长是 cm.
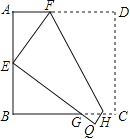
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在绿化某县城与高速公路的连接路段中,需购买罗汉松、雪松两种树苗共400株,罗汉松树苗每株60元,雪松树苗每株70元.相关资料表明:罗汉松、雪松树苗的成活率分别为70%,90%.
(1)若购买这两种树苗共用去26500元,则罗汉松、雪松树苗各购买多少株?
(2)绿化工程来年一般都要将死树补上新苗,现要使该两种树苗来年共补苗不多于80株,则罗汉松树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,才能使购买树苗的费用最低?请求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC,BD交于点O,且AC⊥BC,点E是BC延长线上一点, ![]() ,连接DE.
,连接DE.
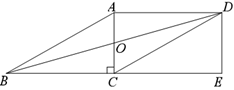
(1)求证:四边形ACED为矩形;
(2)连接OE,如果BD=10,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com