
ЁОЬтФПЁПдкТЬЛЏФГЯиГЧгыИпЫйЙЋТЗЕФСЌНгТЗЖЮжаЃЌашЙКТђТоККЫЩЁЂбЉЫЩСНжжЪїУчЙВ400жъЃЌТоККЫЩЪїУчУПжъ60дЊЃЌбЉЫЩЪїУчУПжъ70дЊЃЎЯрЙизЪСЯБэУїЃКТоККЫЩЁЂбЉЫЩЪїУчЕФГЩЛюТЪЗжБ№ЮЊ70%ЃЌ90%ЃЎ
ЃЈ1ЃЉШєЙКТђетСНжжЪїУчЙВгУШЅ26500дЊЃЌдђТоККЫЩЁЂбЉЫЩЪїУчИїЙКТђЖрЩйжъ?
ЃЈ2ЃЉТЬЛЏЙЄГЬРДФъвЛАуЖМвЊНЋЫРЪїВЙЩЯаТУчЃЌЯжвЊЪЙИУСНжжЪїУчРДФъЙВВЙУчВЛЖргк80жъЃЌдђТоККЫЩЪїУчжСЖрЙКТђЖрЩйжъ?
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌгІШчКЮбЁЙКЪїУчЃЌВХФмЪЙЙКТђЪїУчЕФЗбгУзюЕЭ?ЧыЧѓГізюЕЭЗбгУЃЎ
ЁОД№АИЁПЃЈ1ЃЉЙКТђТоККЫЩЪїУч150жъЃЌбЉЫЩЪїУч250жъЃЛЃЈ2ЃЉТоККЫЩЪїУчжСЖрЙКТђ200жъЃЛЃЈ3ЃЉбЁЙКТоККЫЩЪїУч200жъЃЌбЉЫЩЪїУч200жъЪБЃЌзмЗбгУзюЕЭЃЌЮЊ26000дЊ
ЁОНтЮіЁП
ЩшЙКТђТоККЫЩЪїУчxжъЃЌбЉЫЩЪїУчyжъЃЌ
(1)ИљОнСНжжЪїУчЕФжъЪ§КЭЗбгУСаГіЖўдЊвЛДЮЗНГЬзщЃЌШЛКѓЧѓНтМДПЩЃЛ
(2)ИљОнТоККЫЩЪїУчЕФжъЪ§БэЪОГібЉЫЩЪїУчЮЊ(400-x)жъЃЌШЛКѓИљОнГЩЛюЕФСНжжЪїУчЪ§СаГіВЛЕШЪНЃЌЧѓНтМДПЩЃЛ
(3)БэЪОГіСНжжЪїУчЕФЗбгУЪ§ЃЌШЛКѓИљОнвЛДЮКЏЪ§ЕФдіМѕадЧѓГіЗбгУзюаЁжЕМДПЩЃЎ
(1)ЩшЙКТђТоККЫЩЪїУч![]() жъЃЌбЉЫЩЪїУчyжъЃЌдђ
жъЃЌбЉЫЩЪїУчyжъЃЌдђ
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
Д№ЃКЙКТђТоККЫЩЪїУч150жъ,бЉЫЩЪїУч250жъЃЛ
(2) ЩшЙКТђТоККЫЩЪїУч![]() жъЃЌдђЙКТђбЉЫЩЪїУч
жъЃЌдђЙКТђбЉЫЩЪїУч![]() жъЃЌ
жъЃЌ
гЩЬтвтЕУЃЌ![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
Д№ЃКТоККЫЩЪїУчжСЖрЙКТђ200жъЃЛ
(3)ЩшТоККЫЩЪїУчЙКТђ![]() жъЃЌЙКТђЪїУчЕФЗбгУЮЊ
жъЃЌЙКТђЪїУчЕФЗбгУЮЊ![]() дЊЃЌ
дЊЃЌ
дђга![]() ЃЌ
ЃЌ
ЯдШЛ![]() ЪЧЙигк
ЪЧЙигк![]() ЕФвЛДЮКЏЪ§ЃЌ
ЕФвЛДЮКЏЪ§ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁЃЌ
ЕФдіДѓЖјМѕаЁЃЌ
ЙЪЕБ![]() ШЁзюДѓжЕЪБЃЌ
ШЁзюДѓжЕЪБЃЌ![]() зюаЁЃЌ
зюаЁЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюаЁжЕЃЌЧв
ШЁЕУзюаЁжЕЃЌЧв![]() зюаЁ
зюаЁ![]() ЃЎ
ЃЎ
Д№ЃКЕБбЁЙКТоККЫЩЪїУч200жъЃЌбЉЫЩЪїУч200жъЪБЃЌзмЗбгУзюЕЭЃЌЮЊ26000дЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
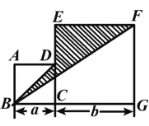
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDгыECGFЪЧСНИіБпГЄЗжБ№ЮЊaЁЂbЕФе§ЗНаЮЃЌ
ЃЈ1ЃЉгУaЁЂbБэЪОЁїBGFЕФУцЛ§ЕФДњЪ§ЪНS1=
ЃЈ2ЃЉЕБa=4cmЁЂb=6cmЪБЃЌЧѓЁїBGFЕФУцЛ§ЃЎ
ЃЈ3ЃЉЧѓГівѕгАВПЗжЕФУцЛ§ЕФДњЪ§ЪНS2 ЃЈгУaЁЂbБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊx=Љ3ЪЧЙигкxЕФЗНГЬЃЈk+3ЃЉx+2=3xЉ2kЕФНтЃЎ
ЃЈ1ЃЉЧѓkЕФжЕЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌвбжЊЯпЖЮAB=6cmЃЌЕуCЪЧжБЯпABЩЯвЛЕуЃЌЧвBC=kACЃЌШєЕуDЪЧACЕФжаЕуЃЌЧѓЯпЖЮCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЧЙтГїОпЕъЙКНјЕчЗЙьвКЭЕчбЙЙјСНжжЕчЦїНјааЯњЪлЃЌЦфНјМлгыЪлМлШчБэЃК
НјМлЃЈдЊ/ЬЈЃЉ | ЪлМлЃЈдЊ/ЬЈЃЉ | |
ЕчЗЙьв | 200 | 250 |
ЕчбЙЙј | 160 | 200 |
ЃЈ1ЃЉвЛМОЖШЃЌГїОпЕъЙКНјетСНжжЕчЦїЙВ30ЬЈЃЌгУШЅСЫ5600дЊЃЌВЂЧвШЋВПЪлЭъЃЌЮЪГїОпЕъдкИУТђТєжазЌСЫЖрЩйЧЎЃП
ЃЈ2ЃЉЮЊСЫТњзуЪаГЁашЧѓЃЌЖўМОЖШГїОпЕъОіЖЈгУВЛГЌЙ§9000дЊЕФзЪН№ВЩЙКЕчЗЙьвКЭЕчбЙЙјЙВ50ЬЈЃЌЧвЕчЗЙьвЕФЪ§СПВЛЩйгкЕчбЙЙјЕФ ![]() ЃЌЮЪГїОпЕъгаФФМИжжНјЛѕЗНАИЃПВЂЫЕУїРэгЩЃЛ
ЃЌЮЪГїОпЕъгаФФМИжжНјЛѕЗНАИЃПВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЧыФуЭЈЙ§МЦЫуХаЖЯЃЌФФжжНјЛѕЗНАИГїОпЕъзЌЧЎзюЖрЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЁїABC ЕФШ§ИіЖЅЕуЕФЮЛжУШчЭМЫљЪОЃЌЕу AЁфЕФзјБъЪЧ(-2ЃЌ2)ЃЌЯжНЋЁїABC ЦНвЦЃЌЪЙЕу A БфЛЛЮЊЕу AЁфЃЌЕу BЁфЁЂCЁфЗжБ№ЪЧ BЁЂC ЕФЖдгІЕуЃЎ
(1) ЧыЛГіЦНвЦКѓЕФЁїAЁфBЁфCЁф(ВЛаДЛЗЈ)ЃЌВЂжБНгаДГіЕуBЁфЁЂCЁфЕФзјБъЃКBЁф ЁЂCЁф ЃЛ
(2) ШєЁїABC ФкВПвЛЕу P ЕФзјБъЮЊ(![]() ЃЌ
ЃЌ![]() )ЃЌдђЕу P ЕФЖдгІЕу PЁфЕФзјБъЪЧ ЃЛ
)ЃЌдђЕу P ЕФЖдгІЕу PЁфЕФзјБъЪЧ ЃЛ
(3) СЌНг AЁфBЃЌCCЁфЃЌВЂЧѓЫФБпаЮ AЁфBCCЁфЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОХЃЈ1ЃЉАрЭЌбЇЮЊСЫНт2011ФъФГаЁЧјМвЭЅдТОљгУЫЎЧщПіЃЌЫцЛњЕїВщСЫИУаЁЧјВПЗжМвЭЅЃЌВЂНЋЕїВщЪ§ОнНјааШчЯТећРэЃЎЧыНтД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉАбЩЯУцЕФЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉШєИУаЁЧјгУЫЎСПВЛГЌЙ§15tЕФМвЭЅеМБЛЕїВщМвЭЅзмЪ§ЕФАйЗжБШЃЛ
ЃЈ3ЃЉШєИУаЁЧјга1000ЛЇМвЭЅЃЌИљОнЕїВщЪ§ОнЙРМЦЃЌИУаЁЧјдТОљгУЫЎСПГЌЙ§20tЕФМвЭЅДѓдМгаЖрЩйЛЇЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌЧвDEЁЮACЃЌAEЁЮBDЃЎЧѓжЄЃКЫФБпаЮAODEЪЧОиаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
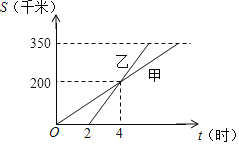
ЁОЬтФПЁПШчЭМЃЌМзЁЂввСНШЫРћгУВЛЭЌЕФНЛЭЈЙЄОпЃЌбиЭЌвЛТЗЯпДгAЕиГіЗЂЕНОрРыAЕи350ЧЇУзЕФBЕиАьЪТЃЌМзЯШГіЗЂЃЌввКѓГіЗЂЃЌМзЁЂввСНШЫОрAЕиЕФТЗГЬКЭЪБМфЕФЙиЯЕШчЭМЫљЪОЃЌИљОнЭМЪОЬсЙЉЕФаХЯЂНтД№ЃК
![]() ввБШМзЭэ______аЁЪБГіЗЂЃЛввГіЗЂ______аЁЪБКѓзЗЩЯМзЃЛ
ввБШМзЭэ______аЁЪБГіЗЂЃЛввГіЗЂ______аЁЪБКѓзЗЩЯМзЃЛ
![]() ЗжБ№ЧѓМзЁЂввСНШЫРыПЊAЕиЕФТЗГЬsЙигкtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЗжБ№ЧѓМзЁЂввСНШЫРыПЊAЕиЕФТЗГЬsЙигкtЕФКЏЪ§ЙиЯЕЪНЃЛ
![]() ЧѓввБШМздчМИаЁЪБЕНДяBЕиЃП
ЧѓввБШМздчМИаЁЪБЕНДяBЕиЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇдкШЋаЃбЇЩњжаПЊеЙСЫЁАЕиЧђЉЮвУЧЕФМвдАЁБЮЊжїЬтЕФЛЗБЃеїЮФБШШќЃЌЦРбЁГівЛЁЂЖўЁЂШ§ЕШНБКЭгХауНБЃЌИљОнНБЯюЕФЧщПіЛцжЦГЩШчЭМЫљЪОЕФСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭМжаЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉИУаЃЛёНБЕФзмШЫЪ§ЮЊ ЃЌ ВЂАбЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉЧѓдкЩШаЮЭГМЦЭМжаБэЪОЁАЖўЕШНБЁБЕФЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЛёЕУвЛЕШНБЕФ4УћбЇЩњжага3Фа1ХЎЃЌЯжДђЫуДгжаЫцЛњбЁГі2УћбЇЩњВЮМгАфНБЛюЖЏЃЌЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓбЁГіЕФ2УћбЇЩњЧЁКУЪЧ1Фа1ХЎЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com