
【题目】如图,在![]() 中,
中,![]() 是
是![]() 外角
外角![]() 的角平分线,反向延长
的角平分线,反向延长![]() 与线段
与线段![]() 延长线交于点
延长线交于点![]() 过
过![]() 作
作![]() 于点
于点![]() 将
将![]() 旋转,得到
旋转,得到![]() 为
为![]() 与
与![]() 的交点,
的交点,![]() 为
为![]() 与
与![]() 延长线的交点,现有以下结论:
延长线的交点,现有以下结论:
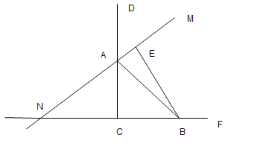
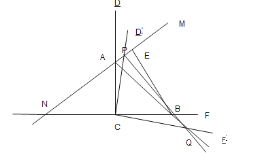
![]() ;
;
![]() 若
若![]() ;
;
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若
若![]() 且
且![]() 时,
时,![]() .
.
其中正确的结论是_____________________(填写所有正确结论的序号).
【答案】![]()
【解析】
延长BE交CD于点K,证明三角形AEK于三角形AEB全等即可判断结论①正确与否;证明![]() 即可推出
即可推出![]() ,由此判断结论②;在
,由此判断结论②;在![]() 中,可得AB的长,根据
中,可得AB的长,根据![]() 求解判断结论③;求出直线AN、AB的解析式,设直线CP的解析式为
求解判断结论③;求出直线AN、AB的解析式,设直线CP的解析式为![]() ,直线CQ的解析式为
,直线CQ的解析式为![]() ,利用方程组求出P、Q坐标,构建方程求出k的值,再求出PQ即可判断结论④.
,利用方程组求出P、Q坐标,构建方程求出k的值,再求出PQ即可判断结论④.
解:①延长BE交CD于点K,

可证明![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
故结论①正确;
②∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
故结论②错误;
③在![]() 中,
中,![]() ,
,
∵![]()
∴![]()
故结论③正确;
④由结论③可知,![]() ,
,![]()
∴![]()
∴![]()
∴直线AN的解析式为:![]() ,直线AB的解析式为:
,直线AB的解析式为:![]()
设直线CP的解析式为![]() ,则直线CQ的解析式为
,则直线CQ的解析式为![]() ,
,
据此可得出![]()
由![]() ,得到
,得到![]()
解得,![]() 或
或![]() (舍去)
(舍去)
∴![]()
∴![]()
结论④错误;
故答案为:①③.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A、F、C、D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE.
(1)求证:△ABC≌△DEF;
(2)若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.
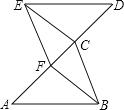
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题7分)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为![]() (即AB:BC=
(即AB:BC=![]() ),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
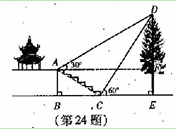
查看答案和解析>>
科目:初中数学 来源: 题型:
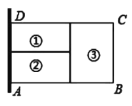
【题目】为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为![]() 的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则
的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则![]() 长为______时,能围成的矩形区域
长为______时,能围成的矩形区域![]() 的面积最大.
的面积最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
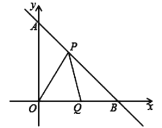
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,动点
两点,动点![]() 在线段
在线段![]() 上移动(与
上移动(与![]() 不重合),以
不重合),以![]() 为顶点作
为顶点作![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)求证:![]() .
.
(3)是否存在点![]() 使得
使得![]() 是等腰三角形?若存在,请直接写出点
是等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
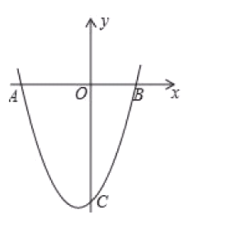
【题目】已知抛物线![]() 的对称轴与
的对称轴与![]() 轴的交点横坐标是分式方程
轴的交点横坐标是分式方程![]() 的解,若抛物线与
的解,若抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ,与
,与![]() 轴的交点
轴的交点![]()
(1)求抛物线![]() 的解析式;
的解析式;
(2)若点![]() 坐标为
坐标为![]() ,连结
,连结![]() ,若点
,若点![]() 是线段
是线段![]() 上的一个动点,求
上的一个动点,求![]() 的最小值.
的最小值.
(3)连结![]() 过点
过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 在第三象限中的抛物线上取点
在第三象限中的抛物线上取点![]() 过点
过点![]() 作直线
作直线![]() 的垂线交直线
的垂线交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,已知
,已知![]() .
.
①求点![]() 的坐标;
的坐标;
②在抛物线上是否存在一点![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
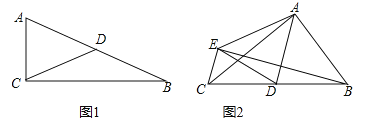
【题目】阅读理解:我们学习过直角三角形斜边上的中线等于斜边的一半,即:如图1,在![]() 中,
中,![]() ,若点
,若点![]() 是斜边
是斜边![]() 的中点,则
的中点,则![]()
灵活应用:如图2,![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() 连接
连接![]() .
.
(1)线段![]() 的长是 ;
的长是 ;
(2)判断![]() 的形状并说明理由;
的形状并说明理由;
(3)线段![]() 的长是 .
的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图正方形![]() 的顶点
的顶点![]() 是
是![]() 和
和![]() 上的动点,与
上的动点,与![]() 交于P、Q两点,
交于P、Q两点,![]() .
.
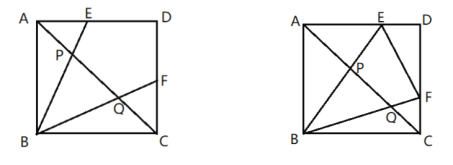
(1)当![]() 时,
时,
①求![]() 的度数;
的度数;
②求以![]() 为边长的正方形面积;
为边长的正方形面积;
(2)当![]() 在
在![]() 上运动时,始终保持
上运动时,始终保持![]() ,连接
,连接![]() ,则
,则![]() 面积的最小值为 (直接写出答案).
面积的最小值为 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON及其边上一点A,以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C,再以点C为圆心,AC长为半径画弧,恰好经过点B,错误的结论是( ).
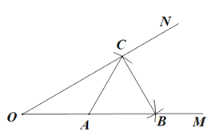
A.![]() B.∠OCB=90°C.∠MON=30°D.OC=2BC
B.∠OCB=90°C.∠MON=30°D.OC=2BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com