
【题目】如图,平行四边形ABCD中,对角线AC,BD交于点O,且AC⊥BC,点E是BC延长线上一点, ![]() ,连接DE.
,连接DE.
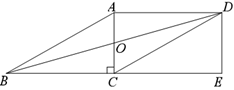
(1)求证:四边形ACED为矩形;
(2)连接OE,如果BD=10,求OE的长.
【答案】(1)证明见解析;(2)OE=5.
【解析】
(1)由题干可知四边形ABCD是平行四边形,且![]() ,可证明四边形ACED是平行四边形,又AC⊥BC,可证明四边形ACED是矩形;
,可证明四边形ACED是平行四边形,又AC⊥BC,可证明四边形ACED是矩形;
(2)由(1)可得∠E=90°,在Rt△ADE中根据定理可得,OE=![]() BD,根据BD的长度可计算出OE的长度.
BD,根据BD的长度可计算出OE的长度.
(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,![]() ,又∵
,又∵![]() ,∴AD=CE∴四边形ABCD是平行四边形,又∵
,∴AD=CE∴四边形ABCD是平行四边形,又∵![]() ,∴∠ACE=90°,∴四边形ACED是矩形.
,∴∠ACE=90°,∴四边形ACED是矩形.
(2)∵对角线AC,BD交于点O,∴点O是BD的中点,∵四边形ACED是矩形,∴∠E=90°,在Rt△ADE中根据定理可得OE=![]() BD,又∵BD=10,∴ OE=5,故答案为5.
BD,又∵BD=10,∴ OE=5,故答案为5.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图正方形![]() 的顶点
的顶点![]() 是
是![]() 和
和![]() 上的动点,与
上的动点,与![]() 交于P、Q两点,
交于P、Q两点,![]() .
.
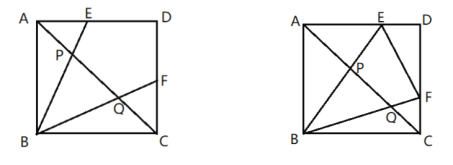
(1)当![]() 时,
时,
①求![]() 的度数;
的度数;
②求以![]() 为边长的正方形面积;
为边长的正方形面积;
(2)当![]() 在
在![]() 上运动时,始终保持
上运动时,始终保持![]() ,连接
,连接![]() ,则
,则![]() 面积的最小值为 (直接写出答案).
面积的最小值为 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON及其边上一点A,以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C,再以点C为圆心,AC长为半径画弧,恰好经过点B,错误的结论是( ).
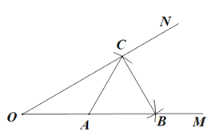
A.![]() B.∠OCB=90°C.∠MON=30°D.OC=2BC
B.∠OCB=90°C.∠MON=30°D.OC=2BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,如果等边三角形的一边与
中,如果等边三角形的一边与![]() 轴平行或在
轴平行或在![]() 轴上,则称这个等边三角形为水平正三角形.
轴上,则称这个等边三角形为水平正三角形.
(1)已知![]() ,
,![]() ,若
,若![]() 是水平正三角形,则点
是水平正三角形,则点![]() 坐标的是_____(只填序号);①
坐标的是_____(只填序号);①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]()
(2)已知点![]() ,
,![]() ,
,![]() ,以这三个点中的两个点及平面内的另一个点
,以这三个点中的两个点及平面内的另一个点![]() 为顶点,构成一个水平正三角形,则这两个点是 ,并求出此时点
为顶点,构成一个水平正三角形,则这两个点是 ,并求出此时点![]() 的坐标;
的坐标;
(3)已知![]() 的半径为
的半径为![]() ,点
,点![]() 是
是![]() 上一点,点
上一点,点![]() 是直线
是直线![]() 上一点,若某个水平正三角形的两个顶点为
上一点,若某个水平正三角形的两个顶点为![]() ,
,![]() ,直接写出点
,直接写出点![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点![]() 、
、![]() 在直线
在直线![]() 上,且
上,且![]() ,
,![]() 于
于![]() 点,且
点,且![]() ,以
,以![]() 为直径在
为直径在![]() 的左侧作半圆
的左侧作半圆![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,
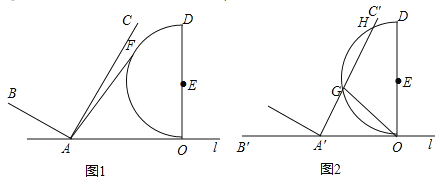
(1)若半圆![]() 上有一点
上有一点![]() ,则
,则![]() 的最大值为__________,最小值为__________;
的最大值为__________,最小值为__________;
(2)向右沿直线![]() 平移
平移![]() 得到
得到![]() ;
;
①如图2,若![]() 截半圆
截半圆![]() 的弧
的弧![]() 的长为
的长为![]() ,求
,求![]() 的度数;
的度数;
②当半圆![]() 与
与![]() 的边相切时,求平移距离.
的边相切时,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图1,在![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上任意一点,
上任意一点,![]() 是等边三角形,且点
是等边三角形,且点![]() 在
在![]() 的内部,连接
的内部,连接![]() .探究线段
.探究线段![]() 与
与![]() 之间的数量关系.
之间的数量关系.
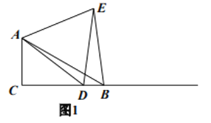
请你完成下列探究过程:
先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.
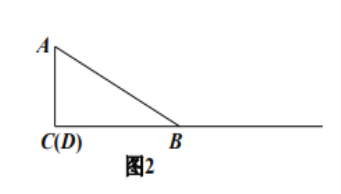
![]() 当点
当点![]() 与点
与点![]() 重合时(如图2),请你补全图形.由
重合时(如图2),请你补全图形.由![]() 的度数为_______________,点
的度数为_______________,点![]() 落在_______________,容易得出
落在_______________,容易得出![]() 与
与![]() 之间的数量关系为_______________
之间的数量关系为_______________
![]() 当
当![]() 是
是![]() 的平分线时,判断
的平分线时,判断![]() 与
与![]() 之间的数量关系并证明
之间的数量关系并证明
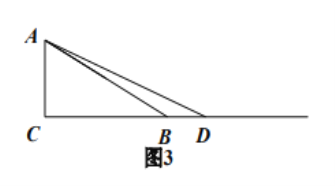
![]() 当点
当点![]() 在如图3的位置时,请你画出图形,研究
在如图3的位置时,请你画出图形,研究![]() 三点是否在以
三点是否在以![]() 为圆心的同一个圆上,写出你的猜想并加以证明.
为圆心的同一个圆上,写出你的猜想并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育看台侧面的示意图如图所示,观众区AC的坡度i为1:2,顶端C离水平地面AB的高度为10m,从顶棚的D处看E处的仰角α=18°30′,竖直的立杆上C、D两点间的距离为4m,E处到观众区底端A处的水平距离AF为3m.
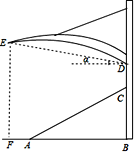
求:(1)观众区的水平宽度AB;
(2)顶棚的E处离地面的高度EF.(sin18°30′≈0.32,tanl8°30′≈0.33,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行射击比赛,两人4次射击的成绩(单位:环)如下:
甲:8,6,9,9;
乙:7,8,9,8.
(1)请将下表补充完整:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | 1.5 | ||
乙 | 8 | 8 |
(2)谁的成绩较稳定?为什么?
(3)分别从甲、乙两人的成绩中随机各选取一次,则选取的两个成绩之和为16环的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
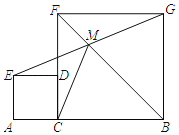
【题目】如图,线段AB=4,点C为线段AB上任意一点(与端点不重合),分别以AC、BC为边在AB的同侧作正方形ACDE和正方形CBGF,分别连接BF、EG交于点M,连接CM,设AC=x,S四边形ACME=y,则y与x的函数表达式为y=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com