
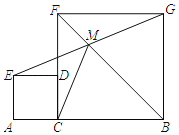
【题目】如图,线段AB=4,点C为线段AB上任意一点(与端点不重合),分别以AC、BC为边在AB的同侧作正方形ACDE和正方形CBGF,分别连接BF、EG交于点M,连接CM,设AC=x,S四边形ACME=y,则y与x的函数表达式为y=_____.
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC,BD交于点O,且AC⊥BC,点E是BC延长线上一点, ![]() ,连接DE.
,连接DE.
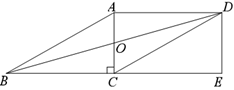
(1)求证:四边形ACED为矩形;
(2)连接OE,如果BD=10,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
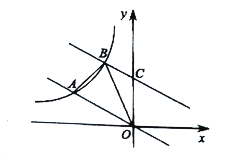
【题目】如图,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 在第二象限内的图象相交于点
在第二象限内的图象相交于点![]() .
.
(1)求反比例函数的解析式;
(2)将直线![]() 向上平移后与反比例函数图象在第二象限内交于点
向上平移后与反比例函数图象在第二象限内交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
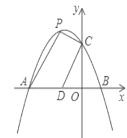
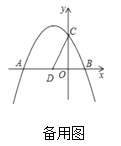
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .已知点
.已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为第二象限内抛物线上的一个动点,连接
为第二象限内抛物线上的一个动点,连接![]() 、
、![]() 、
、![]() .
.
(1)求这个抛物线的表达式.
(2)当四边形![]() 面积等于4时,求点
面积等于4时,求点![]() 的坐标.
的坐标.
(3)①点![]() 在平面内,当
在平面内,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,直接写出满足条件的所有点
为斜边的等腰直角三角形时,直接写出满足条件的所有点![]() 的坐标;
的坐标;
②在①的条件下,点![]() 在抛物线对称轴上,当
在抛物线对称轴上,当![]() 时,直接写出满足条件的所有点
时,直接写出满足条件的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣4,8)和点B(2,n)在抛物线y=ax2上.
(Ⅰ)求该抛物线的解析式和顶点坐标,并求出n的值;
(Ⅱ)求点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求此时点Q的坐标;
(Ⅲ)平移抛物线y=ax2,记平移后点A的对应点为A',点B的对应点为B',点C(﹣2,0)是x轴上的定点.
①当抛物线向左平移到某个位置时,A'C+CB'最短,求此时抛物线的解析式;
②D(﹣4,0)是x轴上的定点,当抛物线向左平移到某个位置时,四边形A'B'CD的周长最短,求此时抛物线的解析式(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
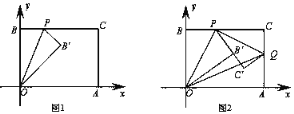
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
(1)如图1,当∠BOP=30°时,求点P的坐标;
(2)如图2,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,设AQ=m,试用含有t的式子表示m;
(3)在(2)的条件下,连接OQ,当OQ取得最小值时,求点Q的坐标;
(4)在(2)的条件下,点C′能否落在边OA上?如果能,直接写出点P的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
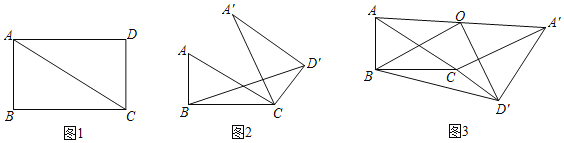
【题目】如图1,ABCD为正方形,将正方形的边CB绕点C顺时针旋转到CE,记∠BCE=α,连接BE,DE,过点C作CF⊥DE于F,交直线BE于H.
(1)当α=60°时,如图1,则∠BHC= ;
(2)当45°<α<90°,如图2,线段BH、EH、CH之间存在一种特定的数量关系,请你通过探究,写出这个关系式: (不需证明);
(3)当90°<α<180°,其它条件不变(如图3),(2)中的关系式是否还成立?若成立,说明理由;若不成立,写出你认为成立的结论,并简要证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,∠ACB=30°,将△ACD绕C点顺时针旋转α(0°<α<360°)至△A'CD'位置.
(1)如图2,若AB=2,α=30°,求S△BCD′.
(2)如图3,取AA′中点O,连OB、OD′、BD′.若△OBD′存在,试判定△OBD′的形状.
(3)当α=α1时,OB=OD′,则α1= °;当α=α2时,△OBD′不存在,则α2= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月28日,由世界月季联合会、中国花卉协会中国花卉协会月季分会主办的“2019世界月季洲际大会暨第九届中国月季展”在河南阳开幕.来自澳大利亚、比利时、智利、芬兰等![]() 个国家的专家学者和其他各界人士共襄盛会,交流月季裁培造景、育种、文化等方面的研究进展及成果.为了解该市民对月季展的关注情况(选项分为:“A.——高度关注”,“B.——般关”.“C.——关注度低”,“D——不关注”,某校兴趣小组随机采访该市部分市民,对采访情况制作了如下不完整的统计图表.
个国家的专家学者和其他各界人士共襄盛会,交流月季裁培造景、育种、文化等方面的研究进展及成果.为了解该市民对月季展的关注情况(选项分为:“A.——高度关注”,“B.——般关”.“C.——关注度低”,“D——不关注”,某校兴趣小组随机采访该市部分市民,对采访情况制作了如下不完整的统计图表.
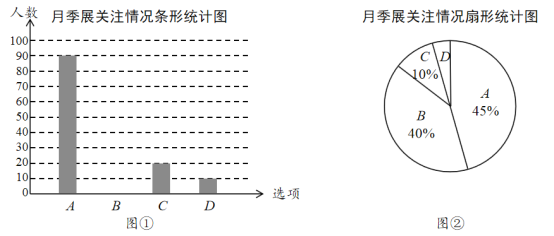
根据以上统计图,解答下列问题:
![]() 本次接受采访的市民共有 人;
本次接受采访的市民共有 人;
![]() 在扇形统计图中,扇形
在扇形统计图中,扇形![]() 的圆心角的度数是 ;
的圆心角的度数是 ;
![]() 请补全条形统计图;
请补全条形统计图;
![]() 若该市区有
若该市区有![]() 万人,根据采访结果,估计不关注月季展市民的人数.
万人,根据采访结果,估计不关注月季展市民的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com