
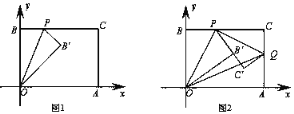
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
(1)如图1,当∠BOP=30°时,求点P的坐标;
(2)如图2,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,设AQ=m,试用含有t的式子表示m;
(3)在(2)的条件下,连接OQ,当OQ取得最小值时,求点Q的坐标;
(4)在(2)的条件下,点C′能否落在边OA上?如果能,直接写出点P的坐标;如果不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)点C′不能落在边OA上.
;(4)点C′不能落在边OA上.
【解析】
(1)在Rt△OBP中,∠BOP=30°,求PB,即求P点坐标;
(2)证明OBP∽△PCQ,得到![]() 即可求解;
即可求解;
(3)OQ2=OA2+AQ2=42+AQ2=16+AQ2,当AQ最短时,OQ最短;
(4)假设点C′能落在边OA上,在Rt△OB′C′中,B′O2+B′C′2=OC′2,32+(4﹣2t)2=(4﹣t)2,△=(﹣8)2﹣4×3×9<0,该方程无实数解,点C′不能落在边OA上.
解:(1)∵A(4,0),B(0,3),
∴OA=4,OB=3,
在Rt△OBP中,
∵∠BOP=30°,
∴PB=![]() ,
,
∴点P的坐标为(![]() ,3),
,3),
(2)由题意,得BP=t,PC=4﹣t,CQ=3﹣m,
由折叠可知:∠OPB=∠OPB′,∠CPQ=∠C′PQ,
又∵∠OPB+∠OPB′+∠CPQ+∠C′PQ=180°,
∴∠OPB+∠CPQ=90°,
又∵∠OPB+∠BOP=90°,
∴∠OPB=∠CPQ,
又∵∠OBP=∠C=90°,
∴△OBP∽△PCQ,
∴![]() ,
,
![]() ,
,
∴m=![]() t2﹣
t2﹣![]() t+3;
t+3;
(3)∵OQ2=OA2+AQ2=42+AQ2=16+AQ2,
∴当AQ最短时,OQ最短,
∵AQ=m=![]() t2﹣
t2﹣![]() t+3=
t+3=![]() (t﹣2)2+
(t﹣2)2+![]() ,
,
∴当t=2时,AQ最短,OQ最短,
此时点Q(4,![]() ),
),
(4)点C′不能落在边OA上,
理由:假设点C′能落在边OA上,由折叠可得
PB=PB′=t,PC=PC′=4﹣t,OB=OB′=3,∠OPB=∠OPC′,∠OB′P=∠OBP=90°,
∵BC∥OA,
∴∠BPO=∠POC′,
∴∠OPC′=∠POC′,
∴OC′=PC′=4﹣t,
∴B′C′=PC﹣PB′=(4﹣t)﹣t=4﹣2t,
在Rt△OB′C′中,∵B′O2+B′C′2=OC′2,
∴32+(4﹣2t)2=(4﹣t)2,
整理,得3t2﹣8t+9=0,
∵△=(﹣8)2﹣4×3×9<0,
∴该方程无实数解,
∴点C′不能落在边OA上.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
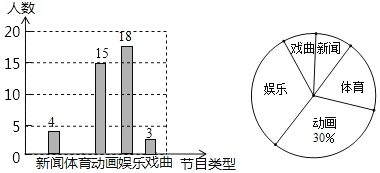
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?并将条形统计图补充完整;
(2)在扇形统计图中,“体育”对应的圆心角的度数是?
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
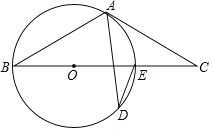
【题目】如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点.
(1)若∠ADE=25°,求∠C的度数;
(2)若AB=AC,CE=2,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
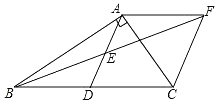
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:四边形ADCF是菱形;
(2)若AC=12,AB=16,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
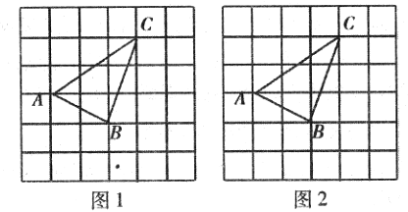
【题目】如图,是由6![]() 6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,请仅用无刻度的直尺,按下列要求画图.
6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,请仅用无刻度的直尺,按下列要求画图.
(1)在图1中找一个格点D,使以点A、B、C、D为顶点的四边形是平行四边形(画出一种情况即可)
(2)在图2中仅用无刻度的直尺,把线段AB三等分(保留画图痕迹,不写画法)
查看答案和解析>>
科目:初中数学 来源: 题型:
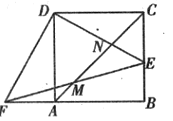
【题目】边长为4的正方形ABCD中,点E是BC边上的一个动点,连接DE,交AC于点N,过点D作DF⊥DE,交BA的延长线于点F,连接EF,交AC于点M.
(1)判定△DFE的形状,并说明理由;
(2)设CE=x,△AMF的面积为y,求y与x之间的函数关系式;并求出当x为何值时y有最大值?最大值是多少?
(3)随着点E在BC边上运动,NA·MC的值是否会发生变化?若不变,请求出NA·MC的值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
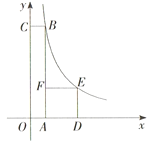
【题目】如图,在平面直角坐标系中,四边形![]() 是矩形,四边形
是矩形,四边形![]() 是正方形,点
是正方形,点![]() 、
、![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 上,点
上,点![]() 、
、![]() 在函数
在函数![]() 的图象上,若正方形
的图象上,若正方形![]() 的面积为4,且
的面积为4,且![]() ,则
,则![]() 的值为( )
的值为( )
A.24B.12C.6D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新冠肺炎在全球蔓延,粮食安全与国际粮食贸易等问题再次引起广泛的关注,2020年4月4日,国务院联防联控机制召开新闻发布会,介绍疫情期间粮食供给和保障工作情况,农业农村部发展规划司魏百刚给出了定心丸:“我国粮食连年丰收,已连续5年稳定在1.3万亿斤以上,口粮保障绝对安全”,1.3万亿用科学记数法表示为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com