
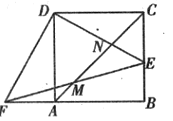
【题目】边长为4的正方形ABCD中,点E是BC边上的一个动点,连接DE,交AC于点N,过点D作DF⊥DE,交BA的延长线于点F,连接EF,交AC于点M.
(1)判定△DFE的形状,并说明理由;
(2)设CE=x,△AMF的面积为y,求y与x之间的函数关系式;并求出当x为何值时y有最大值?最大值是多少?
(3)随着点E在BC边上运动,NA·MC的值是否会发生变化?若不变,请求出NA·MC的值;若变化,请说明理由.
【答案】(1)等腰直角三角形,见解析;(2)y =﹣![]() x2+ x,当x=2,y有最大值1;(3)不变,16
x2+ x,当x=2,y有最大值1;(3)不变,16
【解析】
(1)先判断出∠FDA=∠CDE,证得△ADF≌△CDE,即可得出结论;
(2)利用平行线分线段成比例定理得出比例式表示出AF边上的高,即可得出结论;
(3)先判断出△FAM≌△EIM,得出ME=FM,再判断出△AND∽△CDM,即可得出结论.
(1)在正方形ABCD中,AD=CD,∠ADC=∠DCB=∠DAB =90°,
∵∠FDE=∠ADC=90°,
∴∠FDA=∠CDE,
在△ADF和△CDE中,
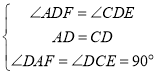 ,
,
∴△ADF≌△CDE,
∴DE =DF,
∴△DFE为等腰直角三角形;
(2)过M作MG⊥AB于G,
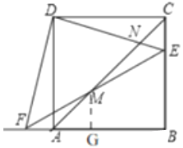
设MG=h,
又∵∠GAM =45°,
∴AG =MG=h,由(1)知FA=CE =![]() ,
,
∵CB⊥AB,
∴MG//BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴h=![]() ,
,
∴y =![]()
![]() ·
·![]() =
=![]()
![]()
![]()
![]() (
(![]() );
);
![]() ,
,
∵![]() ,
,
∴当![]() ,
,![]() 有最大值1;
有最大值1;
(3)不变,如图3,过点E作EI∥AB交AC于I,连接DM,
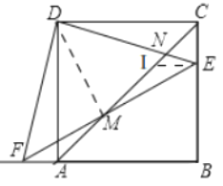
∴∠EIC=∠ICE=45°,
∴EI=EC=AF,
∵EI∥AB,
∴∠FAM=∠MIE,∠MFA=∠IEM,
∴△FAM≌△EIM,
∴ME=FM,
由(1)可得,△FDE是等腰直角三角形,
∴DM⊥EF,
∴∠MDE=45°,∠MDC=45°+∠CDN=∠DNA,
∵∠DAN=∠DCM=45°,
∴△AND∽△CDM,
∴![]() ,
,
∴ANCM=ADCD=16.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
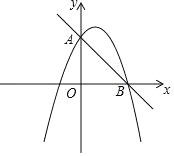
【题目】如图,直线y=﹣x+4与抛物线y=﹣![]() x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.
x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.
(1)求抛物线的解析式;
(2)在x轴下方的抛物线上存在一点P,使得∠ABP=90°,求出点P坐标;
(3)点E是抛物线对称轴上一点,点F是抛物线上一点,是否存在点E和点F使得以点E,F,B,O为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
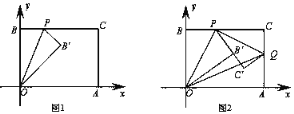
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
(1)如图1,当∠BOP=30°时,求点P的坐标;
(2)如图2,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,设AQ=m,试用含有t的式子表示m;
(3)在(2)的条件下,连接OQ,当OQ取得最小值时,求点Q的坐标;
(4)在(2)的条件下,点C′能否落在边OA上?如果能,直接写出点P的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
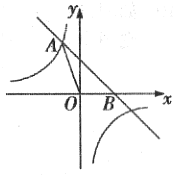
【题目】如图,直线y=﹣x+2与反比例函数y=![]() 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.
(1)求该反比例函数的表达式;
(2)写出直线y=﹣x+2向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年疫情期间,为了更好地落实“停课不停学”行动,我市某中学为了更好督促学生学习,组织教师对某班学生进行家访,根据学生参加网络学习效果划分为![]() (差),
(差),![]() (中),
(中),![]() (优),
(优),![]() (良)四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;
(良)四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;
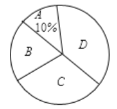
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 等级对应扇形圆心角的度数;
等级对应扇形圆心角的度数;
(3)学校要从![]() 等级的学生中随机选取2人参加李老师个性化辅导,用列表或画树状图求
等级的学生中随机选取2人参加李老师个性化辅导,用列表或画树状图求![]() 等级中的学生小慧被选中参加辅导的概率.
等级中的学生小慧被选中参加辅导的概率.
效果等级 | 频数 | 频率 |
| 5 | |
| ||
|
| 0.3 |
| 20 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将函数![]() 的图象位于
的图象位于![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折至其上方后,所得的是新函数
轴翻折至其上方后,所得的是新函数![]() 的图象.若该新函数图象与直线
的图象.若该新函数图象与直线![]() 有两个交点,则
有两个交点,则![]() 的取值范围为___________.
的取值范围为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8,P是线段BC上任意一点,以点P为圆心PB为半径的圆与线段AB相交于点Q(点Q与点A、B不重合),∠CPQ的角平分线与AC相交于点D.
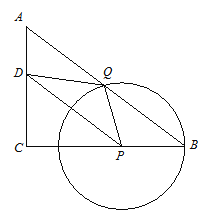
(1)如果DQ=PB,求证:四边形BQDP是平行四边形;
(2)设PB=x,△DPQ的面积为y,求y关于x的函数关系式,并写出x的取值范围;
(3)如果△ADQ是以DQ为腰的等腰三角形,求PB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com