
【题目】已知点A(﹣4,8)和点B(2,n)在抛物线y=ax2上.
(Ⅰ)求该抛物线的解析式和顶点坐标,并求出n的值;
(Ⅱ)求点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求此时点Q的坐标;
(Ⅲ)平移抛物线y=ax2,记平移后点A的对应点为A',点B的对应点为B',点C(﹣2,0)是x轴上的定点.
①当抛物线向左平移到某个位置时,A'C+CB'最短,求此时抛物线的解析式;
②D(﹣4,0)是x轴上的定点,当抛物线向左平移到某个位置时,四边形A'B'CD的周长最短,求此时抛物线的解析式(直接写出结果即可).
【答案】(I)y=![]() ;(0,0);2;(II)P(2,﹣2);Q(
;(0,0);2;(II)P(2,﹣2);Q(![]() ,0);(III)①y=
,0);(III)①y=![]() (x+
(x+![]() )2;②y=
)2;②y=![]() (x+
(x+![]() )2.
)2.
【解析】
(I)把(﹣4,8)代入y=ax2可求得a的值,可得抛物线的解析式,这条抛物线的顶点是原点,把x=2代入所求的抛物线解析式,可得n的值;
(II)求得AP与x轴的交点即为Q的坐标;
(III)①先计算CQ的长,可知平移的距离和方向,用顶点式设出相应的函数解析式,把新顶点坐标代入即可;
②左右平移时,使A′D+DB′′最短即可,那么作出点A′关于x轴对称点的坐标为A′′,得到直线A′′B′′的解析式,将点D的坐标代入,可得b的值,同理用顶点式设出相应的函数解析式,把新顶点坐标代入即可.
解:(I)将点A(﹣4,8)的坐标代入y=ax2,
解得a=![]() ,
,
∴抛物线的解析式是y=![]() ,顶点坐标是(0,0),
,顶点坐标是(0,0),
将点B(2,n)的坐标代入y=![]() x2,得n=
x2,得n=![]() =2;
=2;
(II)由(I)知:点B的坐标为(2,2),
则点B关于x轴对称点P的坐标为(2,﹣2),
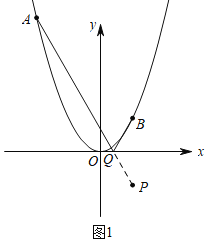
如图1,连接AP与x轴的交点为Q,此时AQ+BQ最小,
设直线AP的解析式为y=kx+b,![]() ,
,
解得: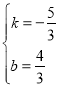
∴直线AP的解析式是y=﹣![]() x+
x+![]() ,
,
令y=0,得x=![]() ,
,
即所求点Q的坐标是(![]() ,0);
,0);
(III)①∵点C(﹣2,0),点Q的坐标是( ![]() ,0)
,0)
∴CQ=![]() ﹣(﹣2)=
﹣(﹣2)=![]() ,
,
故将抛物线y=![]() x2向左平移
x2向左平移![]() 个单位时,A′C+CB′最短,
个单位时,A′C+CB′最短,
此时抛物线的函数解析式为y=![]() (x+
(x+![]() )2;
)2;
②左右平移抛物线y=![]() x2,
x2,
∵线段A′B′和CD的长是定值,
∴要使四边形A′B′CD的周长最短,只要使A′D+CB′最短;
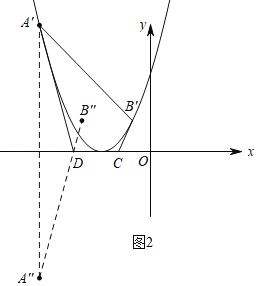
第一种情况:如果将抛物线向右平移,显然有A′D+CB′在增大,
∴不存在某个位置,使四边形A′B′CD的周长最短;
第二种情况:设抛物线向左平移了b个单位,如图2,
则点A′和点B′的坐标分别为A′(﹣4﹣b,8)和B′(2﹣b,2).
∵CD=2,
∴将点B′向左平移2个单位得B′′(﹣b,2),要使A′D+CB′最短,只要使A′D+DB′′最短,
∵点A′关于x轴对称点的坐标为A′′(﹣4﹣b,﹣8),
由A'和B'两点的坐标得:直线A′′B′′的解析式为y=![]() x+
x+![]() b+2.
b+2.
要使A′D+DB′′最短,点D应在直线A′′B′′上,
将点D(﹣4,0)代入直线A′′B′′的解析式,解得b=![]() .
.
∴将抛物线向左平移时,存在某个位置,使四边形A′B′CD的周长最短,
此时抛物线的函数解析式为y=![]() (x+
(x+![]() )2.
)2.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知点![]() 、
、![]() 在直线
在直线![]() 上,且
上,且![]() ,
,![]() 于
于![]() 点,且
点,且![]() ,以
,以![]() 为直径在
为直径在![]() 的左侧作半圆
的左侧作半圆![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,
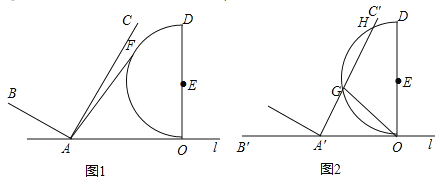
(1)若半圆![]() 上有一点
上有一点![]() ,则
,则![]() 的最大值为__________,最小值为__________;
的最大值为__________,最小值为__________;
(2)向右沿直线![]() 平移
平移![]() 得到
得到![]() ;
;
①如图2,若![]() 截半圆
截半圆![]() 的弧
的弧![]() 的长为
的长为![]() ,求
,求![]() 的度数;
的度数;
②当半圆![]() 与
与![]() 的边相切时,求平移距离.
的边相切时,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
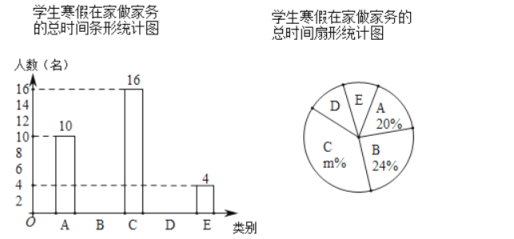
根据统计图提供的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)扇形统计图中m的值是 ,类别D所对应的扇形圆心角的度数是 度;
(4)若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=4,点C为线段AB上任意一点(与端点不重合),分别以AC、BC为边在AB的同侧作正方形ACDE和正方形CBGF,分别连接BF、EG交于点M,连接CM,设AC=x,S四边形ACME=y,则y与x的函数表达式为y=_____.
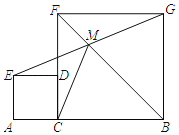
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD交于点O,且AC⊥BD,AC=BD,SABCD=8cm2,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为F,连接DF,则下列四个结论中,错误的是( )
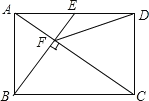
A. △AEF~△CABB. CF=2AFC. DF=DCD. tan∠CAD=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点;
(3)在(2)的条件下,若△ABC的边长为1,直接写出EF的最大值.
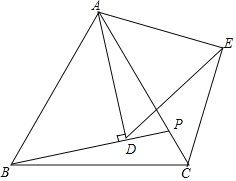
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com